Layers

Linear Layer (Fully Connected Layer)

$$z=Wx+b$$

Gradient w.r.t weights

$$\frac{\partial \mathcal{L}}{\partial W}=\frac{\partial \mathcal{L}}{\partial z}\cdot x^T$$

Gradient w.r.t bias

$$\frac{\partial \mathcal{L}}{\partial b}=\frac{\partial \mathcal{L}}{\partial z}$$

Gradient w.r.t input of the linear layer (to be passed backwards to earlier layers)

$$\frac{\partial \mathcal{L}}{\partial x}=W^T\cdot \frac{\partial \mathcal{L}}{\partial z}$$

Convolutional Layer (1D Case)

For 1D convolution with input length $n$, kernel length $k$, output length $m=n-k+1$:

$$z_i=\sum _{j=1}^k{w}_j\cdot x_{i+j-1}+b,i\in 1,...,m$$

Bias gradient: Given that

$$\frac{\partial \mathcal{L}}{\partial z}=\left[{\delta }_1,{\delta }_2,\dots ,{\delta }_m\right]$$

And so

$$\frac{\partial \mathcal{L}}{\partial b}=\sum _{i=1}^m{\delta }_i$$

Kernel gradient:

$$\frac{\partial \mathcal{L}}{\partial w_j}=\sum _{i=1}^m{\delta }_i\cdot x_{i+j-1},j\in 1,...,k$$

Input gradient:

$$\frac{\partial \mathcal{L}}{\partial x_p}=\sum _{i=\max (1,p-k+1)}^{\min (m,p)}{\delta }_i\cdot w_{p-i+1},p\in 1,...,n$$

Convolutional Layer (2D Case)

Here, I’m going to generalize to any dimensional convolution to 2D since that’s when its used. $z$ → $Z$ which is a tensor, $x$ → $X$ which is a tensor, $W$ is the weight matricies we use for convolutions AKA kernels.

$$Z=W\ast X+b$$ $$Z_{i,j,c}=\sum _{m,n,d}{W}_{m,n,d,c}\cdot X_{i+m,j+n,d}+b_c$$

Where $\ast$ is the convolution operator. $i,j$ are spatial indicies, $m,n$ are spatial indicies of the kernel, $d$ is the input channel index, $c$, is the output channel index. Basically, we shift around a kernel over an input and compute the sum of the element-wise multiplication of the kernel and the area in the input.

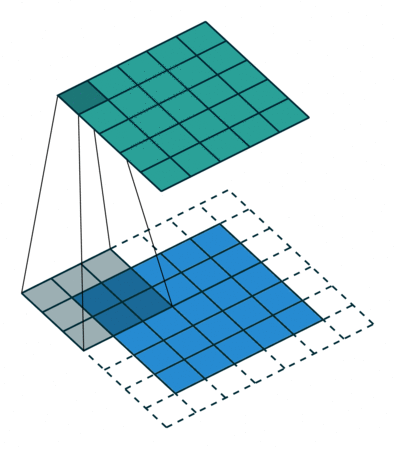
Gradient w.r.t kernel weights. We convolve the gradient over the input

$$\frac{\partial \mathcal{L}}{\partial W_{m,n,d,c}}=\sum _{i,j}\frac{\partial \mathcal{L}}{\partial Z_{i,j,c}}\cdot X_{i+m,j+n,d}$$

Gradient w.r.t input. We convolve the gradient with a 180 degree horizontally flipped kernel

$$\frac{\partial \mathcal{L}}{\partial X_{i,j,d}}=\sum _{m,n,c}\frac{\partial \mathcal{L}}{\partial Z_{i-m,j-n,c}}\cdot W_{m,n,d,c}$$

Gradient w.r.t bias. We sum the incoming gradient over that specific input channel

$$\frac{\partial \mathcal{L}}{\partial b_c}=\sum _{i,j}\frac{\partial \mathcal{L}}{\partial Z_{i,j,c}}$$

Scaled Dot-Product Attention

$$\text{Attention}(Q,K,V)=\text{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$

where:

• $Q=X{W}_Q$ (queries)
• $K=X{W}_K$ (keys)
• $V=X{W}_V$ (values)
• $A=\text{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)$ (attention weights)

Backward:

This is the most complex. Given $\frac{\partial \mathcal{L}}{\partial \text{out}}$:

Gradient w.r.t. $V$:

$$\frac{\partial \mathcal{L}}{\partial V}=A^T\cdot \frac{\partial \mathcal{L}}{\partial \text{out}}$$

Gradient w.r.t. attention weights $A$:

$$\frac{\partial \mathcal{L}}{\partial A}=\frac{\partial \mathcal{L}}{\partial \text{out}}\cdot V^T$$

Gradient through softmax: Let $S=\frac{Q{K}^T}{\sqrt{d_k}}$ (pre-softmax scores)

$$\frac{\partial \mathcal{L}}{\partial S}=A\odot \left(\frac{\partial \mathcal{L}}{\partial A}-\text{rowsum}\left(\frac{\partial \mathcal{L}}{\partial A}\odot A\right)\right)$$

(This comes from the softmax Jacobian - messy but necessary)

Gradient w.r.t. $Q$ and $K$:

$$\frac{\partial \mathcal{L}}{\partial Q}=\frac{1}{\sqrt{d_k}}\cdot \frac{\partial \mathcal{L}}{\partial S}\cdot K$$ $$\frac{\partial \mathcal{L}}{\partial K}=\frac{1}{\sqrt{d_k}}\cdot {\frac{\partial \mathcal{L}}{\partial S}}^T\cdot Q$$

Finally, gradients w.r.t. weight matrices:

$$\frac{\partial \mathcal{L}}{\partial W_Q}=X^T\cdot \frac{\partial \mathcal{L}}{\partial Q}$$ $$\frac{\partial \mathcal{L}}{\partial W_K}=X^T\cdot \frac{\partial \mathcal{L}}{\partial K}$$ $$\frac{\partial \mathcal{L}}{\partial W_V}=X^T\cdot \frac{\partial \mathcal{L}}{\partial V}$$