Lie Algebra

Its a fundamental concept in mathematics and physics that lets us study the local, linear behaviour of a corresponding non-linear Lie Group at its identity.

This is because as you zoom into a local area on a Lie Group, it becomes linear in nature. THE LINEAR SPACE ABOUT THE IDENTITY IS CALLED THE LIE ALGEBRA.

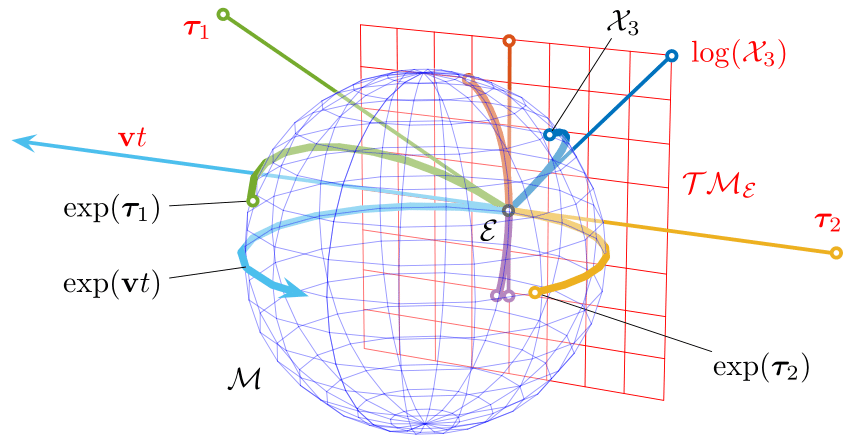
Representation of the relation between the Lie group and the Lie algebra. The Lie algebra (red plane) is the tangent space to the Lie group's manifold (here represented as a blue sphere) at the identity. Through the exponential map, each straight path through the origin on the Lie algebra produces a path over the manifold which runs along the respective geodesic. Conversely, each element of the group has an equivalent in the Lie algebra. This relation is so profound that (nearly) all operations in the group, which is curved and nonlinear, have an exact equivalent in the Lie algebra, which is a linear vector space. Though the sphere in R^3 is not a Lie group (we just use it as a representation that can be drawn on paper), that in R^4 is, and describes the group of unit quaternions.

Exponential and Logarithm

The conversions between the lie algebra and lie group is known as exponential and log.

• exp: Lie Algebra → Lie Group
• log: Lie Group → Lie Algebra

Isomorphisms

When we derive the Lie Algebra, we can end up in a space thats a bit weird to work with (ie. in $S^1$ we end up in the space $i\mathbb{R}$). As a result, we’d like to do a small helper operation that lets us directly handle Lie Algebra ($i\mathbb{R}$, ${\mathbb{R}}^{3\times 3}$) in a Cartesian space ($\mathbb{R}$, ${\mathbb{R}}^6$). These are what we define as the Hat and Vee Operators. It preserves distance

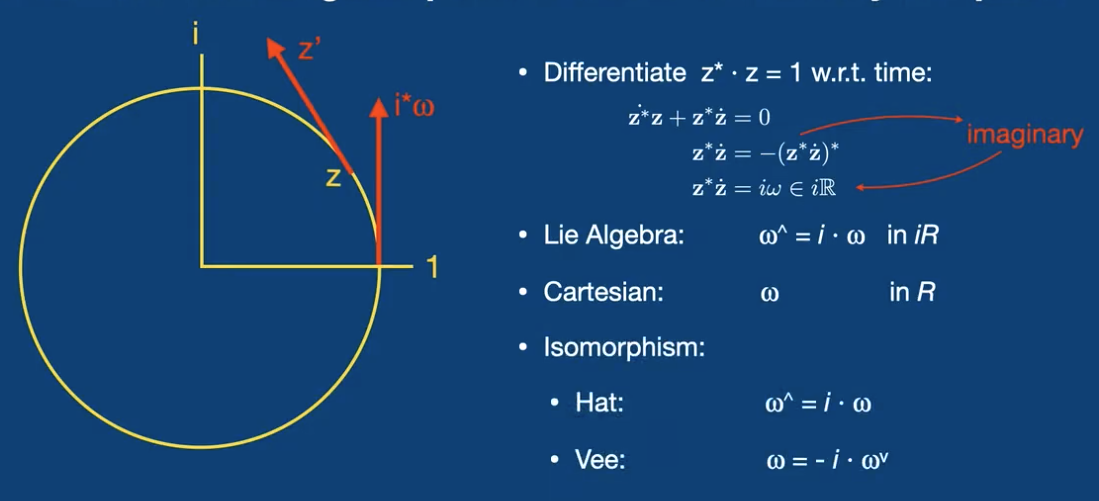
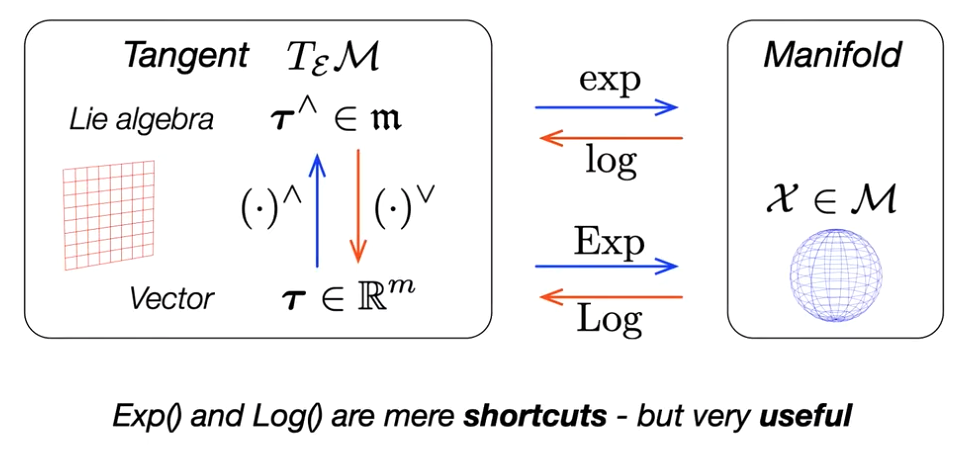
When we do a Vee operation on the Lie Algebra, we end up with a nice Cartesian space to do think in vectors. The corresponding operations to go from this space to the Lie Group is the Exponential and Logarithm (just capitalized).

Plus Minus Operators

There are special operators that we define so that we can equate addition in the Lie Algebra vector space to the resultant associative Lie Group

$$\mathcal{X}\oplus w\triangleq \mathcal{X}\ast Exp(w)$$

$\triangleq$ means defined as, and remember $\ast$ is the operator of the Lie Group

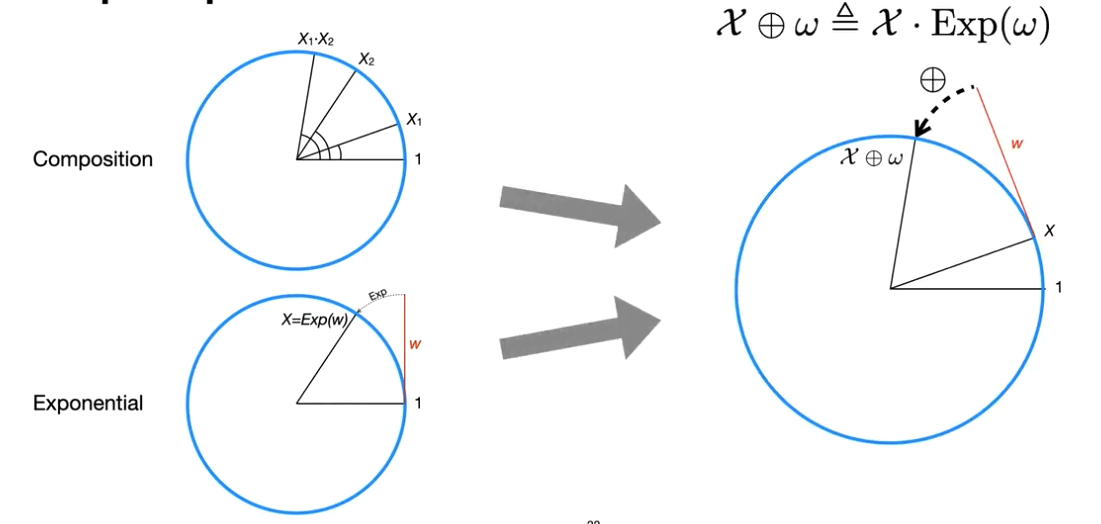
Likewise, there is an equivalent minus operator in Lie Algebra

$$\mathcal{Y}\ominus \mathcal{X}\triangleq Log({\mathcal{X}}^{-1}\ast \mathcal{Y})$$

Adjoint Matrix

From the special plus operator:

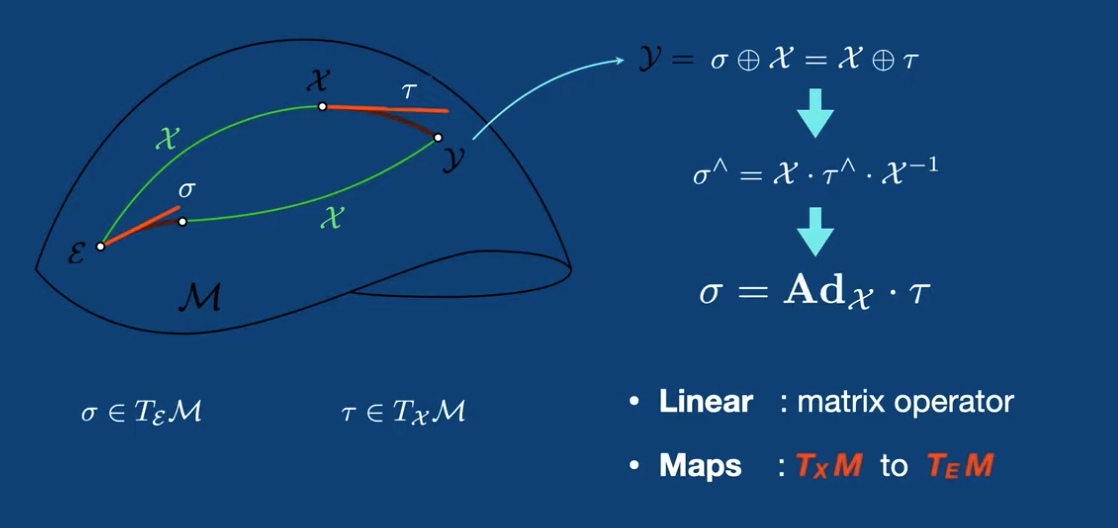
• This means that we have a way to map one vector in Lie Algebra to another.

Calculus on the Lie Group

We can express the operation of two elements in the Lie Group as the operation on two Cartesian vectors in the Lie Algebra! As a result, we can define our own ideas of Jacobian and Covariance in this space.

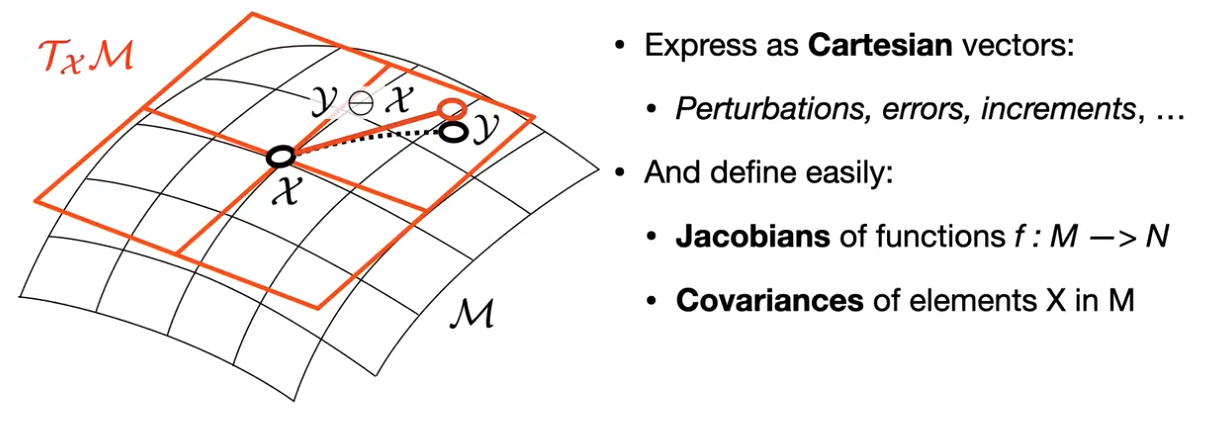
Jacobians in Lie Group

In vector space, we define the Jacobian from first principles as:

$$\mathbf{J}\triangleq \underset{h\to 0}{\lim }\frac{f(\mathbf{x}+\mathbf{h})-f(\mathbf{x})}{\mathbf{h}}\in {\mathbb{R}}^{n\times m}$$

You can define something similar for Jacobians in Lie Algebra:

$$\mathbf{J}\triangleq \underset{\mathbf{\tau }\to 0}{\lim }\frac{f(\mathcal{X}\oplus \mathbf{\tau })\ominus f(\mathcal{X})}{\mathbf{\tau }}\in {\mathbb{R}}^{n\times m}$$

---

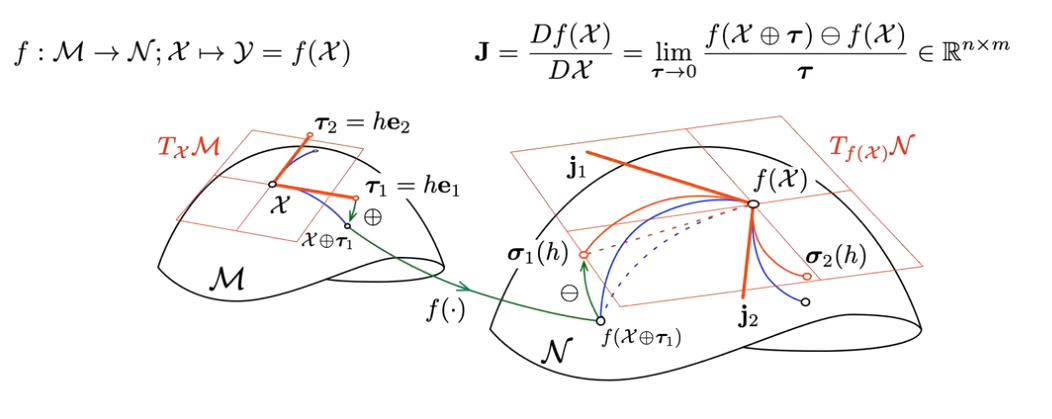
EXAMPLE with SO(3)

Given we have a function $f$ defined as $f:SO(3)\times {\mathbb{R}}^3\to {\mathbb{R}}^3;(\mathbf{R},\mathbf{p})\mapsto f(\mathbf{R},\mathbf{p})=\mathbf{R}\ast \mathbf{p}$

$$\frac{Df}{D\mathbf{R}}=\underset{\mathbf{\theta }\to 0}{\lim }\frac{f(\mathbf{R}\oplus \mathbf{\theta },\mathbf{p})\ominus f(\mathbf{R},\mathbf{p})}{\mathbf{\theta }}=\underset{\theta \to 0}{\lim }\frac{(\mathbf{R}\oplus \mathbf{\theta })\ast \mathbf{p}-\mathbf{R}\ast \mathbf{p}}{\mathbf{\theta }}$$ $$=\underset{\theta \to 0}{\lim }\frac{\mathbf{R}\ast Exp(\mathbf{\theta })\ast \mathbf{p}-\mathbf{R}\ast \mathbf{p}}{\mathbf{\theta }}$$

For SO(3) we can approximate the Exponential map as:

$$Exp(\mathbf{\theta })=\mathbf{I}+{\theta }_{\times }$$

Where ${\theta }_{\times }$ is the skew symmetric matrix.

$${\theta }_{\times }=\left[\begin{array}{ccc}0& -{\theta }_3& {\theta }_2\\ {\theta }_3& 0& -{\theta }_1\\ -{\theta }_2& {\theta }_1& 0\end{array}\right]$$ $$=\underset{\theta \to 0}{\lim }\frac{\mathbf{R}\ast (\mathbf{I}+{\theta }_{\times })\ast \mathbf{p}-\mathbf{R}\ast \mathbf{p}}{\mathbf{\theta }}$$ $$=\underset{\theta \to 0}{\lim }\frac{\mathbf{R}\ast \mathbf{I}\ast \mathbf{p}+\mathbf{R}\ast {\theta }_{\times }\ast \mathbf{p}-\mathbf{R}\ast \mathbf{p}}{\mathbf{\theta }}$$ $$=\underset{\theta \to 0}{\lim }\frac{\mathbf{R}\ast {\theta }_{\times }\ast \mathbf{p}}{\mathbf{\theta }}$$ $$=\underset{\theta \to 0}{\lim }\frac{-\mathbf{R}\ast {\mathbf{p}}_{\times }\ast \mathbf{\theta }}{\mathbf{\theta }}$$

Why? Well we can expand and see:

$${\mathbf{\theta }}_{\times }\cdot \mathbf{p}=\left[\begin{array}{ccc}0& -{\theta }_3& {\theta }_2\\ {\theta }_3& 0& -{\theta }_1\\ -{\theta }_2& {\theta }_1& 0\end{array}\right]\left[\begin{array}{c}{p}_1\\ p_2\\ p_3\end{array}\right]=\left[\begin{array}{c}{\theta }_2{p}_3-{\theta }_3{p}_2\\ {\theta }_3{p}_1-{\theta }_1{p}_3\\ {\theta }_1{p}_2-{\theta }_2{p}_1\end{array}\right]$$ $${\mathbf{p}}_{\times }\cdot \mathbf{\theta }=\left[\begin{array}{ccc}0& -p_3& p_2\\ p_3& 0& -p_1\\ -p_2& p_1& 0\end{array}\right]\left[\begin{array}{c}{\theta }_1\\ {\theta }_2\\ {\theta }_3\end{array}\right]=\left[\begin{array}{c}{p}_2{\theta }_3-p_3{\theta }_2\\ p_3{\theta }_1-p_1{\theta }_3\\ p_1{\theta }_2-p_2{\theta }_1\end{array}\right]$$ $$\text{therefore}{\mathbf{\theta }}_{\times }\cdot \mathbf{p}=-{\mathbf{p}}_{\times }\cdot \mathbf{\theta }$$ $$=-\mathbf{R}\ast {\mathbf{p}}_{\times }$$

---

Differentiation in Lie Groups

Just a couple of notation definitions and some deductions from those definitions.

Pertubation in Lie Groups and Covariance

So moving a little bit LOL.

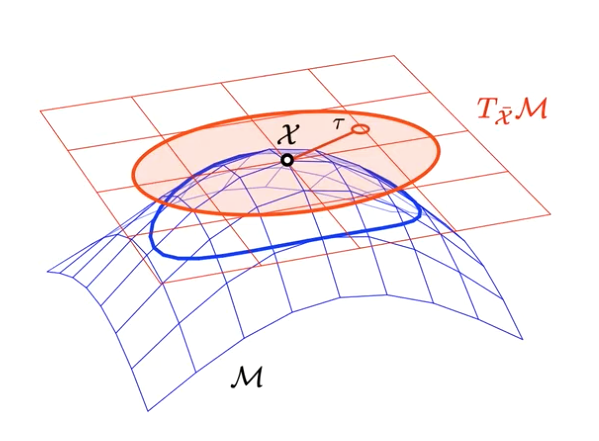
Lets say we define a pertubation in Lie Algebra.

\mathcal{X}=\mathcal{\bar{X}}\oplus \boldsymbol{\tau} \;\;\text{where}\;\;\boldsymbol{\tau} \sim \mathcal{N}(0,\mathbf{P}) $$Where $\tau$ represents some random vector. From there, we can see how covariance comes into play:

\mathbf{P}\triangleq \mathbb{E}[\boldsymbol{\tau}*\boldsymbol{\tau}^{T}]

\mathbf{P}\triangleq\mathbb{E}[(\mathcal{X}\ominus\mathcal{\bar{X}})*(\mathcal{X}\ominus\mathcal{\bar{X}})^{T}]

$$Propagationisprettyeasyonceyoujust"think"inLieAlgebralol.$$

\mathcal{Y}=f(\mathcal{X});;\mathbf{J}=\frac{D\mathcal{Y}}{D\mathcal{X}}

\mathbf{P}{\mathcal{Y}}=\mathbf{J}*\mathbf{P}{\mathcal{X}}*\mathbf{J}^{T}

# Integration in Lie Groups ![[Pasted image 20251106102003.png]]