Manifold

A manifold is a type of Topological Space that locally looks like a flat Euclidean space ${\mathbb{R}}^n$, even though it might look globally curved or complicated.

Formal Definition: Topological Manifold

An $n$-dimensional topological manifold is a topological space $M$ such that:

1. Hausdorff: For any two distinct points $p,q\in M$, there exist disjoint open sets $U,V\subseteq M$ such that $p\in U$ and $q\in V$

2. Second-countable: The topology on $M$ has a countable basis

3. Locally Euclidean of dimension $n$: For every point $p\in M$, there exists an open neighborhood $U\subseteq M$ containing $p$ and a homeomorphism $\varphi :U\to V$ where $V$ is an open subset of ${\mathbb{R}}^n$

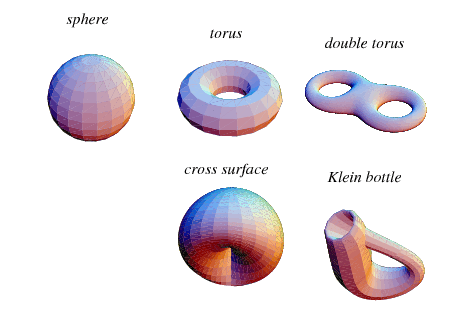
Too far down the rabbit hole, its a smooth looking space.