Perspective Camera

A perspective camera is just an idealized camera model used for our understanding of computer vision. For this, we will be using the frontal projection model (which is a bit different from what you learned awhile ago. Specifically that the projected plane is on the same side as the object.)

TLDR

Given we have points in world frame ${\vec{r}}_{pw}=\left[\begin{array}{c}{x}_w\\ y_w\\ z_w\end{array}\right]$ and the transform between the camera and the world frame is given by

$${\mathbf{T}}_{sw}=\left[\begin{array}{cc}{\mathbf{C}}_{sw}& {\mathbf{t}}_{sw}\end{array}\right]$$

The pinhole camera model is defined as

$$z_s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\mathbf{K}{\mathbf{T}}_{sw}\left[\begin{array}{c}{\vec{r}}_{pw}\\ 1\end{array}\right]$$

Which expanded looks like

$$z_s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}\alpha & \gamma & c_u\\ 0& \beta & c_v\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cc}{\mathbf{C}}_{sw}& {\mathbf{t}}_{sw}\end{array}\right]\left[\begin{array}{c}{x}_w\\ y_w\\ z_w\\ 1\end{array}\right]$$

• $\mathbf{K}$ is our camera intrinsic matrix
  • $\alpha$ is our horizontal focal length accounting for pixel size $\alpha =f_{u}l$
  • $\beta$ is our vertical focal length accounting for pixel size $\beta =f_v$
  • $\gamma$ is our skew coefficient (usually 0)
  • $c_u$ is the horizontal offset to center the image plane with the camera frame
  • $c_v$ is the vertical offset to center the image place with the camera frame
• $\mathbf{T}$ is our camera extrinsic matrix (chopped transformation matrix)
  • $\mathbf{C}$ is a valid rotation matrix
  • $\mathbf{t}$ is our transformation vector
• $z_s$ is the depth of the point in camera frame (must be divided out at the end to get our $u$ and $v$). The act of dividing out the depth is know as perspective projection

Accounting for Distortion

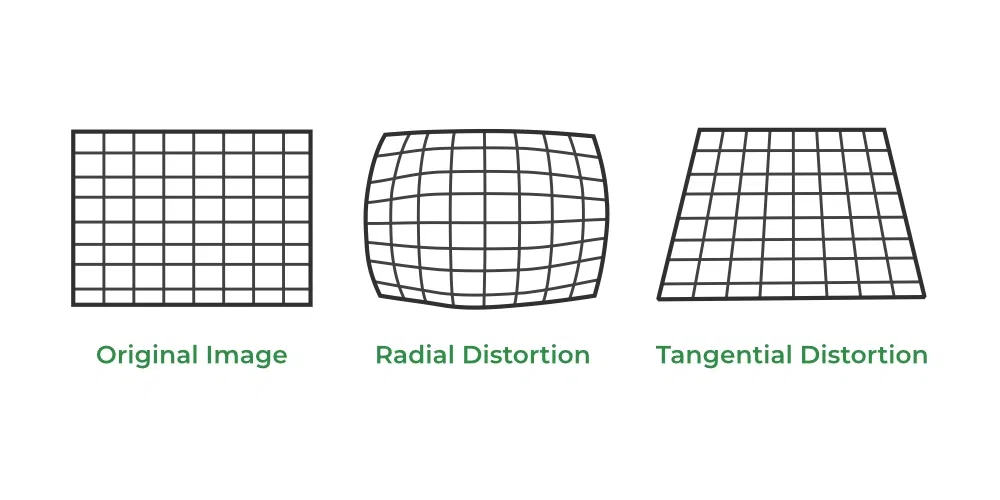Distortion is a non-linear function, and there are number of different models for distortion.

$$D(\cdot ):\left[\begin{array}{c}{x}_n\\ y_n\end{array}\right]\to \left[\begin{array}{c}{x}_d\\ y_d\end{array}\right]$$

Brown-Conrady Distortion Model

AKA Plumb Bob Model

$$x_d=x_n\underset{\text{radial distortion}}{\underbrace{\frac{1+k_1{r}^2+k_2{r}^4+k_3{r}^6}{1+k_4{r}^2+k_5{r}^4+k_6{r}^6}}}+\underset{\text{tangential distortion}}{\underbrace{2p_1{x}_n{y}_n+p_2(r^2+2x_n^2)}}+\underset{\begin{array}{c}\text{thin prism}\\ \text{distortion}\\ \text{(misaligned}\\ \text{lenses)}\end{array}}{\underbrace{s_1{r}^2+s_2{r}^4}}$$ $$y_d=y_n\frac{1+k_1{r}^2+k_2{r}^4+k_3{r}^6}{1+k_4{r}^2+k_5{r}^4+k_6{r}^6}+p_1(r^2+2y_n^2)+2p_2{x}_n{y}_n+s_3{r}^2+s_4{r}^4$$

where

$$r^2=x_n^2+y_n^2$$

This is the distortion model used by OpenCV

However, most of the time OpenCV uses the standard 5-parameter, simplified model for most calibrations.

$$x_d=x_n(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)+2p_1{x}_n{y}_n+p_2(r^2+2x_n^2)$$ $$y_d=y_n(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)+p_1(r^2+2y_n^2)+2p_2{x}_n{y}_n$$

Adding Distortion into the model

We add in the distortion after the extrinsic and perspective transform, before passing through camera intrinsics

$$z_s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}\alpha & \gamma & c_u\\ 0& \beta & c_v\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cc}{\mathbf{C}}_{sw}& {\mathbf{t}}_{sw}\end{array}\right]\left[\begin{array}{c}{x}_w\\ y_w\\ z_w\\ 1\end{array}\right]$$ $$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}\alpha & \gamma & c_u\\ 0& \beta & c_v\\ 0& 0& 1\end{array}\right]D\left(\frac{{\mathbf{T}}_{sw}\left[\begin{array}{c}{\vec{r}}_{pw}\\ 1\end{array}\right]}{z_s}\right)$$

Explanation

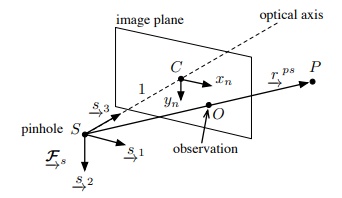
We have our pinhole $S$ and a point in 3D space, $P$. The vector to the point from the pinhole is

$$\rho ={\mathbf{r}}_s^{ps}=\left[\begin{array}{c}x\\ y\\ z\end{array}\right]$$

important to note that the $\overrightarrow{s_3}$ axis is normal to the image plane

The projected point $O$ which will end up on the plane is given by a vector $\mathbf{p}$

$$\mathbf{p}=\left[\begin{array}{c}{x}_n\\ y_n\\ 1\end{array}\right]=\left[\begin{array}{c}\frac{x}{z}\\ \frac{y}{z}\\ 1\end{array}\right]$$

It is homogeneous to work with matrix calculations. This is called a normalized image coordinate

Essential Matrix

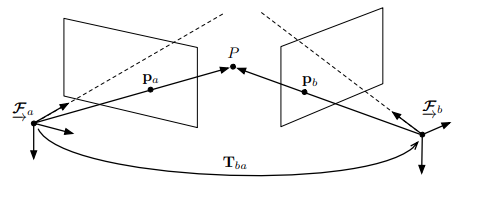If the same point is collected by the same camera after a transformation, the two observations of the same point are related by

$${\mathbf{p}}_a^T{\mathbf{E}}_{ab}{\mathbf{p}}_b=0$$

Where $\mathbf{E}$ is called the essential matrix.

$${\mathbf{E}}_{ab}={\mathbf{C}}_{ba}^T{\mathbf{r}}_b^{ab\wedge }$$

And its related to the pose of the camera

$${\mathbf{T}}_{ba}=\left[\begin{array}{cc}{\mathbf{C}}_{ba}& {\mathbf{r}}_b^{ab}\\ 0^T& 1\end{array}\right]$$

Lens Distortion

It exists, and we need to characterize it and deal with it, This affects how close a real camera is to our idealized model. But once it is characterized, we can run an undistortion procedure to get the camera image to something we can actually use.

Intrinsic Parameters

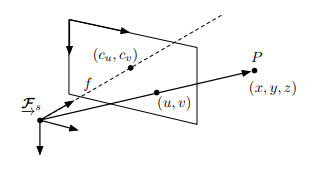We were assuming right before this that the focal length is 1, so we actually need to deal with that (as well as map to pixel coordinates which start from the top left of the image)

$$\mathbf{q}=\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\mathbf{Kp}=\left[\begin{array}{ccc}{f}_u& 0& c_u\\ 0& f_v& c_v\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{x}_n\\ y_n\\ 1\end{array}\right]$$

These have to be determined through camera calibration

Fundamental Matrix

Similar to the Essential Matrix, but defined between two different cameras. Lets say we have two different cameras

$${\mathbf{q}}_a={\mathbf{K}}_a{\mathbf{p}}_a$$ $${\mathbf{q}}_b={\mathbf{K}}_b{\mathbf{p}}_b$$

The fundamental matrix, ${\mathbf{F}}_{ab}$ exists such that

$${\mathbf{q}}_a^T{\mathbf{F}}_{ab}{\mathbf{q}}_b=0\text{where}{\mathbf{F}}_{ab}={\mathbf{K}}_a^{-T}{\mathbf{E}}_{ab}{\mathbf{K}}_b^{-1}$$

Reasoning

$${\mathbf{q}}_a^T{\mathbf{F}}_{ab}{\mathbf{q}}_b={\mathbf{p}}_a^T\underset{1}{\underbrace{{\mathbf{K}}_a^T{\mathbf{K}}_a^{-T}}}{\mathbf{E}}_{ab}\underset{1}{\underbrace{{\mathbf{K}}_b^{-1}{\mathbf{K}}_b}}{\mathbf{p}}_b={\mathbf{p}}_a^T{\mathbf{E}}_{ab}{\mathbf{p}}_b=0$$

The constraint associated with the fundamental matrix is also called the epipolar constraint

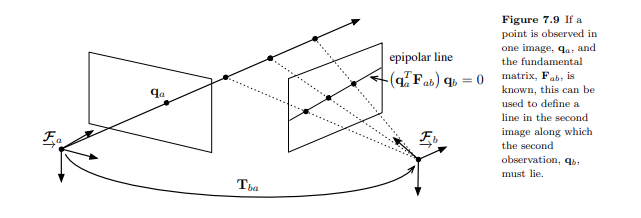
Homography

If an observed point is on a plane of known geometry, it is possible to work out what the point will look like on another camera of a known pose change. This is called homography.

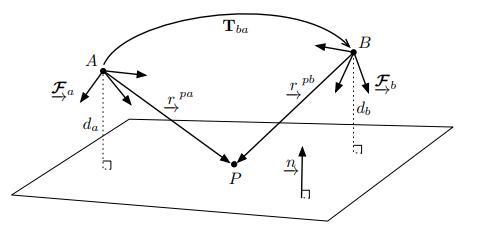
Like before, we have two cameras

$${\mathbf{q}}_a={\mathbf{K}}_a{\mathbf{p}}_a={\mathbf{K}}_a\frac{1}{z_a}{\mathbf{\rho }}_a$$ $${\mathbf{q}}_b={\mathbf{K}}_b{\mathbf{p}}_b={\mathbf{K}}_b\frac{1}{z_b}{\mathbf{\rho }}_b$$

Say we know the equation of the Plane expressed in both camera frames to be

$$\{{\mathbf{n}}_a,d_a\}\text{ and }\{{\mathbf{n}}_b,{\mathbf{d}}_b\}$$

This implies that

$${\mathbf{n}}_a^T{\mathbf{\rho }}_a+d_a=0$$ $${\mathbf{n}}_b^T{\mathbf{\rho }}_b+d_b=0$$

Substituting our equations for $\rho$

$$z_i{\mathbf{n}}_i^T{K}_i^{-1}{\mathbf{q}}_i+d_i=0i=a,b$$ $$\text{or }{z}_i=-\frac{d_i}{{\mathbf{n}}_i^T{\mathbf{K}}_i^{-1}{\mathbf{q}}_i}$$

This implies that we can write the coordinates of $P$ with respect to any camera frame as

$${\mathbf{q}}_i={\mathbf{K}}_i\frac{1}{z_i}{\mathbf{\rho }}_i$$ $${\mathbf{\rho }}_i=z_i{\mathbf{K}}_i^{-1}{\mathbf{q}}_i$$ $${\mathbf{\rho }}_i=-\frac{d_i}{{\mathbf{n}}_i^T{\mathbf{K}}_i^{-1}{\mathbf{q}}_i}{\mathbf{K}}_i^{-1}{\mathbf{q}}_i$$

Extending this to our coodinates in the image plane, we get that

$${\mathbf{q}}_b={\mathbf{K}}_b{\mathbf{H}}_{ba}{\mathbf{K}}_a^{-1}{\mathbf{q}}_a\underset{\text{Homography Matrix }}{\underbrace{{\mathbf{H}}_{ba}=\frac{z_a}{z_b}{\mathbf{C}}_{ba}\left(1+\frac{1}{d_a}{\mathbf{r}}_a^{ba}{\mathbf{n}}_a^T\right)}}$$

The Homography Matrix lets us determine the how a point in one image plane is gonna look like in another plane. Given that we know the geometry of the point

The Homography matrix is invertible

$${\mathbf{H}}_{ba}^{-1}={\mathbf{H}}_{ab}$$