Sigmapoint (Unscented) Transformation

A compromise between linearization techniques like the Extended Kalman Filter and Monte Carlo Method.

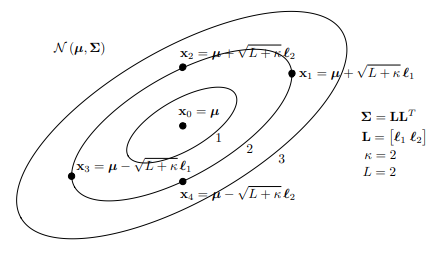
1. A set of $2L+1$ sigmapoints ${\mathbf{x}}_i$ are compute from the input density, $\mathcal{N}({\mathbf{\mu }}_x,{\mathbf{\Sigma }}_{\times })$, according to

$$\mathbf{L}{\mathbf{L}}^T={\mathbf{\Sigma }}_{xx}$$ $${\mathbf{x}}_0={\mathbf{\mu }}_x$$ $${\mathbf{x}}_i={\mathbf{\mu }}_x+\sqrt{L+\mathcal{K}}co{l}_i\mathbf{L}$$ $${\mathbf{x}}_{i+L}={\mathbf{\mu }}_x-\sqrt{L+\mathcal{K}}co{l}_i\mathbf{L}$$

You can convert the sigmapoints back to the distribution by

$${\mathbf{\mu }}_x=\sum _{i=0}^{2L}{\alpha }_i{\mathbf{x}}_i$$ $${\mathbf{\Sigma }}_{xx}=\sum _{i=0}^{2L}{\alpha }_i({\mathbf{x}}_i-{\mathbf{\mu }}_i)({\mathbf{x}}_i-{\mathbf{\mu }}_x{)}^T$$ $${\alpha }_i=\{\begin{array}{ll}\frac{\kappa }{L+\kappa },& i=0\\ \frac{1}{2}\frac{1}{L+\kappa }& otherwise\end{array}$$

$\kappa$ here is a user defined parameter.

$\kappa$ lets you define how far away the sigmapoints are from the mean. It affects the fourth moment of the distribution which is known as kurtosis

where $L=dim({\mathbf{\mu }}_x)$ is the dimensionality of the mean

2. For each sigmapoint , pass it through the nonlinearity

$${\mathbf{y}}_i=\mathbf{g}({\mathbf{x}}_i),i=0\dots 2L$$

3. The mean of the output density is computed as

$${\mathbf{\mu }}_y=\sum _{i=0}^{2L}{\alpha }_i{\mathbf{y}}_i$$

4. The covariance of the output density, ${\mathbf{\Sigma }}_{yy}$, is computed as

$${\mathbf{\Sigma }}_{yy}=\sum _{i=0}^{2L}{\alpha }_i({\mathbf{y}}_i-{\mathbf{\mu }}_y)({\mathbf{y}}_i-{\mathbf{\mu }}_y{)}^T$$

5. The output density $\mathcal{N}({\mathbf{\mu }}_y,{\mathbf{\Sigma }}_{yy})$ is returned

Advantages

1. We can avoid finding the Jacobian of the non-linearity
2. only standard linear algebra operations are employed
3. The computation cost is similar to linearization (when a numerically derived Jacobian is used)
4. There is no requirement that the nonlinearity be smooth and differentiable