see Fourier Series
Learning an Image with Neural Networks
Setup
import torch
from torchvision.io import read_image
import matplotlib.pyplot as plt
IMAGE_WIDTH = 224
IMAGE_HEIGHT = 224
IMAGE_CHANNEL = 1
RGB_MAX = 256
device = "cuda" if torch.cuda.is_available() else "cpu"Loading and Visualizing Image
cat_img = read_image("data/learning_an_image/cat108.jpg")
cat_img_norm = cat_img / RGB_MAX
cat_img_norm, plt.imshow(cat_img_norm.permute(1, 2, 0))
Initial Attempt: Learning Image with CNN
from torch import nn
from torchvision.utils import save_image
LEARNING_RATE = 0.01
EPOCHS = 1000
EVAL_INTERVAL = 50
class CatModel(nn.Module):
def __init__(self, device):
super().__init__()
self.conv0 = nn.Conv2d(in_channels=2, out_channels=64, kernel_size=3, stride=1, padding='same', device=device)
self.conv1 = nn.Conv2d(in_channels=64, out_channels=128, kernel_size=3, stride=1, padding='same', device=device)
self.conv2 = nn.Conv2d(in_channels=128, out_channels=512, kernel_size=3, stride=1, padding='same', device=device)
self.conv4 = nn.Conv2d(in_channels=512, out_channels=3, kernel_size=3, stride=1, padding='same', device=device)
self.relu = nn.ReLU()
def forward(self, x):
x = self.relu(self.conv0(x))
x = self.relu(self.conv1(x))
x = self.relu(self.conv2(x))
return torch.sigmoid(self.conv4(x))
model = CatModel(device)
loss_fn = torch.nn.MSELoss()
opt = torch.optim.SGD(model.parameters(), lr=LEARNING_RATE)
# prepare set of data
image_out = cat_img_norm.to(device)
image_x = torch.arange(0, IMAGE_WIDTH, device=device).unsqueeze(1) * torch.ones(IMAGE_HEIGHT, device=device).unsqueeze(0)
image_y = torch.ones(IMAGE_HEIGHT, device=device).unsqueeze(1) * torch.arange(0, IMAGE_HEIGHT, device=device).unsqueeze(0)
image_in = torch.stack((image_x, image_y))
def train(model, image, cat_img, loss_fn, opt):
model.train()
pred = model(image)
loss = loss_fn(pred, cat_img)
opt.zero_grad()
loss.backward()
opt.step()
print(f"LOSS {loss}")
def show_img(epoch, model, image):
model.eval()
pred = model(image)
pred = pred
for e in range(EPOCHS):
train(model, image_in, image_out, loss_fn, opt)
if e % EVAL_INTERVAL == 0:
with torch.inference_mode():
show_img(e, model, image_in)
pred = model(image_in).detach().cpu().squeeze()
plt.imshow(pred.permute(1, 2, 0))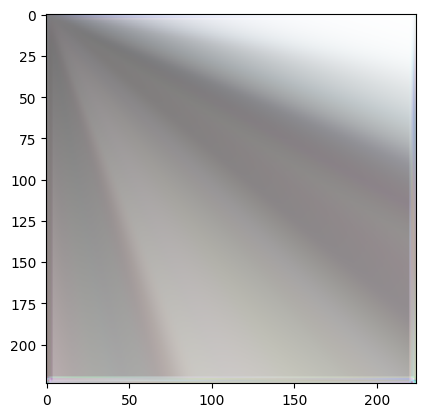
Spectral Bias
This is the tendency for a neural network to bias towards learning low frequency representations of data. As shown above, we ended up learning a “low-frequency” representation of the cat (the colours are there, but no complex patterns were learned).
Regardless of overparameterizing the space, the existence of spectral bias persists. This is a fundamental architectural limitation with most standard activation functions (specifically for ones that do not have some form of frequency parameter built in).
To counteract this, we can add in a Fourier Feature Network (that is, encode our input as fourier features).
Fourier Feature Encoding
import torch
import math
import matplotlib.pyplot as plt
import numpy as np
# Parameters
IMAGE_L = 224
N_FREQ = 20
SIGMA = 10.0
# Creating input
input_range = torch.arange(0, IMAGE_L)
input = torch.stack((input_range.unsqueeze(1) * torch.ones(IMAGE_L).unsqueeze(0),
torch.ones(IMAGE_L).unsqueeze(1) * input_range.unsqueeze(0))) / IMAGE_L
freqs = torch.randn((2, N_FREQ)) * SIGMA
input = input.permute(1, 2, 0) # [224, 224, 2]
input_sin = torch.sin(2*math.pi*(input@freqs)) # [224, 224, 20]
input_cos = torch.cos(2*math.pi*(input@freqs)) # [224, 224, 20]
input_enc = torch.cat((input_sin, input_cos), dim=2) # [224, 224, 40]
input_enc = input_enc.permute(2, 0, 1) # [40, 224, 224]
# Plotting
n_channels = input_enc.shape[0] # 40 channels
n_cols = 8
n_rows = (n_channels + n_cols - 1) // n_cols # Ceiling division
fig, axes = plt.subplots(n_rows, n_cols, figsize=(20, n_rows*2.5))
axes = axes.flatten()
for i in range(n_channels):
axes[i].imshow(input_enc[i].numpy(), cmap='RdBu', vmin=-1, vmax=1)
if i < N_FREQ:
axes[i].set_title(f'sin(freq {i})', fontsize=10)
else:
axes[i].set_title(f'cos(freq {i-N_FREQ})', fontsize=10)
axes[i].axis('off')
# Hide any unused subplots
for i in range(n_channels, len(axes)):
axes[i].axis('off')
plt.tight_layout()
plt.savefig('data/learning_an_image/fourier_features.png', dpi=150, bbox_inches='tight')
plt.show()
print(f"Plotted {n_channels} Fourier feature channels")
print(f"Input encoding shape: {input_enc.shape}")One thing to note here is that we are treating the image as the signal of a single period. This makes the signal periodic funny enough.

Learning Image with Fourier Features
import math
import matplotlib.pyplot as plt
import torch
from torch import nn
from torchmetrics.image import PeakSignalNoiseRatio
from torchvision.io import read_image
# Train a Model, this time by first encoding our input as fourier features
device = "cuda" if torch.cuda.is_available() else "cpu"
RGB_MAX = 256
IMAGE_L = 224
N_FREQ = 128
SIGMA = 10.0
LEARNING_RATE = 2.0
MOMENTUM = 0.9
EPOCHS = 1000
EVAL_INT = 10
# Metrics
psnr = PeakSignalNoiseRatio(data_range=1.0)
# Creating input
input_range = torch.arange(0, IMAGE_L) # [224]
input = torch.stack((input_range.unsqueeze(1) * torch.ones(IMAGE_L).unsqueeze(0), torch.ones(IMAGE_L).unsqueeze(1) * input_range.unsqueeze(0)), dim=2) / IMAGE_L # [224, 224, 2]
freqs = torch.randn((2, N_FREQ)) * SIGMA # [2, N_FREQ]
input_sin = torch.sin(2*math.pi*(input@freqs)) # [224, 224, N_FREQ]
input_cos = torch.cos(2*math.pi*(input@freqs)) # [224, 224, N_FREQ]
input_enc = torch.cat((input_sin, input_cos), dim=2) # [224, 224, 2*N_FREQ]
input_enc = input_enc.permute(2, 0, 1) # [2*N_FREQ, 224, 224]
print(input_enc.shape)
# Creating output
cat_img = read_image("data/learning_an_image/cat108.jpg")
cat_img_norm = cat_img / RGB_MAX
# model
class CatModel(nn.Module):
def __init__(self, device):
super().__init__()
self.conv_block = nn.Sequential(
nn.Conv2d(in_channels=2*N_FREQ, out_channels=128, kernel_size=1, stride=1, padding='same', device=device),
nn.ReLU(),
nn.Conv2d(in_channels=128, out_channels=256, kernel_size=1, stride=1, padding='same', device=device),
nn.ReLU(),
nn.Conv2d(in_channels=256, out_channels=3, kernel_size=1, stride=1, padding='same', device=device)
)
def forward(self, x):
x = self.conv_block(x)
return torch.sigmoid(x)
model = CatModel(device)
loss_fn = torch.nn.MSELoss()
opt = torch.optim.SGD(model.parameters(), lr=LEARNING_RATE, momentum=MOMENTUM)
input_enc = input_enc.to(device)
cat_img_norm = cat_img_norm.to(device)
def train(model, loss_fn, opt, input_enc, cat_img_norm):
model.train()
pred = model(input_enc)
loss = loss_fn(pred, cat_img_norm)
opt.zero_grad()
loss.backward()
opt.step()
def test(model, input_enc, cat_img_norm):
model.eval()
pred = model(input_enc).detach().cpu()
psnr.update(pred, cat_img_norm.detach().cpu())
print(f"PSNR: {psnr.compute(): .2f} dB")
for e in range(EPOCHS):
train(model, loss_fn, opt, input_enc, cat_img_norm)
if e % EVAL_INT == 0:
with torch.inference_mode():
test(model, input_enc, cat_img_norm)
pred = model(input_enc).detach().cpu().squeeze()
pred = (pred * 256).int()
plt.imshow(pred.permute(1, 2, 0))Things to Note
- NNs using simple activation functions are biased towards learning low frequency representations of data, this is known as spectral bias
- To counteract spectral bias, we can encode our input as a Fourier Series consisting of arbitrary harmonic frequencies. Our network can then learn the “weights” of each frequency in the series to approximate the data
- CNNs hardcode specific inductive biases into the network. They include:
- Hierarchy: the output of the network can be built from a set of signal primitives
- Locality: nearby pixels are more related to each other than farther ones
- Translation Equivariance: translating the input will shift the output in a similar way
- Parameter Sharing: the same set of weights (kernel) is applied everywhere in the image
- When we introduce a fourier feature encoding, we are insinuating that the image is some non-linear function of a set of arbitrary sinusoids (this diverges away from simple fourier series because it assumes that we can represent a periodic signal as a sum of sinusoids, the introduction of NN layers here makes this no longer a linear combination)
- Because we made the assumption above, we should use a network that shares parameters, because we are assuming that the non-linear function can be generalized to every pixel. Thus 1D convolution (which implicitly represents an MLP at each pixel)

Optimized Implementation
import torch
from torch import nn
from torchmetrics.image import PeakSignalNoiseRatio
import math
RGB_MAX = 256
IMAGE_HW = 224
LEARNING_RATE = 1.0
MOMENTUM = 0.9
EPOCHS = 2000
EVAL_INT = 100
N_FREQ = 128
SIGMA = 10.0
# Input
input = torch.stack((torch.arange(IMAGE_HW).unsqueeze(1) * torch.ones(IMAGE_HW).unsqueeze(0), torch.ones(IMAGE_HW).unsqueeze(1) * torch.arange(IMAGE_HW).unsqueeze(0)), dim=2) / IMAGE_HW # [224, 224, 2]
input_freq = torch.randn((2, N_FREQ)) * SIGMA # [2, N_FREQ]
input_sin = torch.sin(2*math.pi*input@input_freq) # [224, 224, N_FREQ]
input_cos = torch.cos(2*math.pi*input@input_freq) # [224, 224, N_FREQ]
input_enc = torch.cat((input_sin, input_cos), dim=2) # [224, 224, 2*N_FREQ]
input_enc = input_enc.permute(2, 0, 1) # [2*N_FREQ, 224, 224]
input_enc = input_enc.contiguous() # This actually DOUBLES the speed, so contiguity MATTERS
# Output
cat_img = read_image("data/learning_an_image/cat108.jpg") / RGB_MAX
# Metrics
psnr = PeakSignalNoiseRatio(data_range=1.0)
# Model
class CatModel(nn.Module):
def __init__(self):
super().__init__()
self.conv_block = nn.Sequential(
nn.Conv2d(in_channels=2*N_FREQ, out_channels=128, kernel_size=1, padding='same'),
nn.ReLU(),
nn.Conv2d(in_channels=128, out_channels=256, kernel_size=1, padding='same'),
nn.ReLU(),
nn.Conv2d(in_channels=256, out_channels=3, kernel_size=1, padding='same'),
)
def forward(self, x):
x = self.conv_block(x)
return torch.sigmoid(x)
model = CatModel()
model.cuda()
input_enc = input_enc.to(device)
cat_img = cat_img.to(device)
loss_fn = torch.nn.MSELoss()
opt = torch.optim.SGD(model.parameters(), lr=LEARNING_RATE, momentum=MOMENTUM)
def train(model, loss_fn, opt, input, output):
model.train()
pred = model(input)
loss = loss_fn(pred, output)
opt.zero_grad()
loss.backward()
opt.step()
print(f"LOSS {loss}")
def test(model, input, output):
pred = model(input)
psnr.update(pred.detach().cpu(), cat_img_norm.detach().cpu())
print(f"PSNR: {psnr.compute(): .2f} dB")
for e in range(EPOCHS):
train(model, loss_fn, opt, input_enc, cat_img)
if e % EVAL_INT == 0:
with torch.inference_mode():
test(model, input_enc, cat_img)
pred_final = model(input_enc)
plt.imshow(pred_final.detach().cpu().permute(1, 2, 0))
