Fourier Series

Precursor to the Fourier Transform actually.

It shows that any periodic function can be represented as a superposition of sine and cosine functions as harmonic frequencies.

Mathematical Definition

Given a periodic function $f(t)$ which has a period of $T$

$$f(t)=\frac{a_0}{2}+\sum _{n=1}^{\infty }\left[a_n\cos \left(\frac{2\pi nt}{T}\right)+b_n\sin \left(\frac{2\pi nt}{T}\right)\right]$$

Where coefficients $a_n$ and $b_n$ are found by:

$$a_n=\frac{2}{T}{\int }_0^{T}f(t)\cos \left(\frac{2\pi nt}{T}\right)dt$$ $$b_n=\frac{2}{T}{\int }_0^{T}f(t)\sin \left(\frac{2\pi nt}{T}\right)dt$$

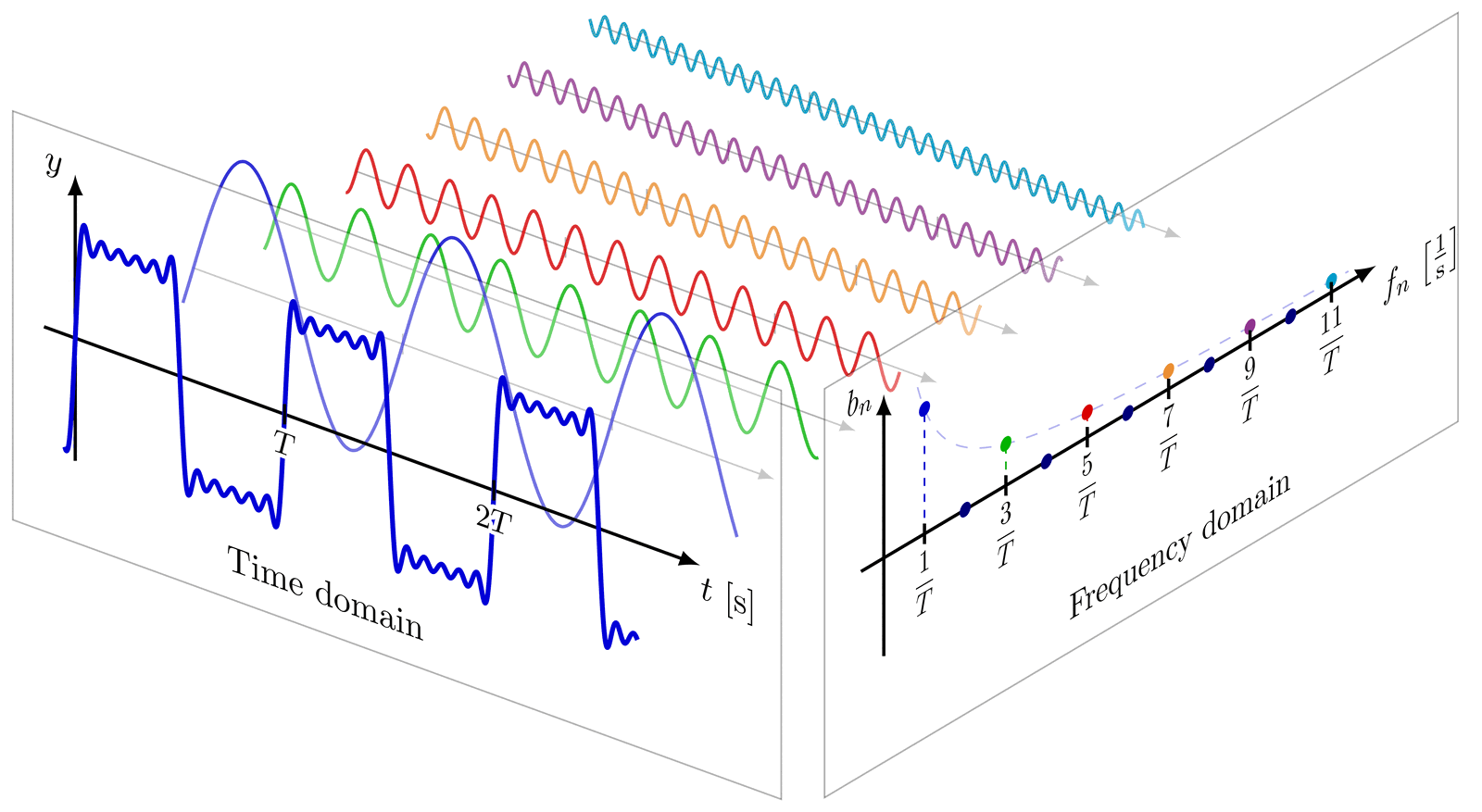
Extension to Non-Periodic

Its pretty simple, you just:

1. pretend that the bounds of your non-periodic function is a single period
2. fit a Fourier Series on that pseudo-periodic function ($T=L$)
3. the series will match $f(t)$ perfectly within the bounds $[0,L]$ and just repeat forever after that.