Fourier Transform

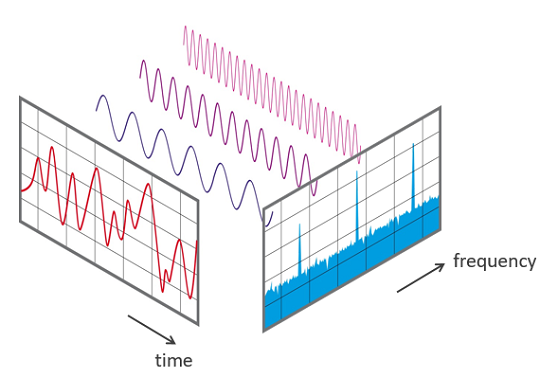
The Fourier Transform comes from the idea that any signal (continuous or discrete) can be represented as a sum of sinusoidal functions at different frequencies (Fourier’s Theorem)

Fourier's Theorem Any periodic signal is composed of a superposition of pure sin waves, with suitably chosen amplitudes and phases.

An extension to Fourier's Theorem is that any signal within a bound can be represented as a superposition of pure sine waves, with suitably chosen amplitudes and phases.

Mathematical Definition

For a continuous function $f(t)$, the Fourier Transform $F(\omega )$ for any frequency $\omega$ is

$$F(\omega )={\int }_{-\infty }^{\infty }f(t)e^{-i\omega t}dt$$

$i=j$ which is the imaginary number (different conventions in mathematics and engineering). Note: the frequency $\omega$ is a value that we set.

The Inverse Fourier Transform is given as

$$f(t)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }F(\omega )e^{i\omega t}dt$$

By Euler’s Formula

$$e^{-i\omega t}=\cos (\omega t)-i\sin (\omega t)$$

Combining both sine and cosine, allowing ups to capture both amplitude and phase at a given frequency $\omega$

The Fourier Transform is the generalized equation of a Fourier Series. Whereas Fourier Series functions on a set of different indexed frequencies, Fourier Transform functions on a continuous set of frequencies $\omega$, or in other words, $\omega$ is an entire axis.

When the function is symmetrical, the Fourier Transform has no imaginary part. Otherwise, the Fourier Transform will witness a imaginary part.

This imaginary part of a Fourier Transform is a necessary evil lol. It’s needed in order for the Fourier Transform to be invertible, and to encode timing.

• People usually don’t analyze the imaginary part in isolation, they either
  • Ignore it entirely (signal processing)
  • Analyze the phase shift (usually shows time delay) and magnitudes (shows the frequency content)