Control Systems

No time for notes right now but the general premise is:

• We have a plant (the thing we are trying to control)
• We have a controller (the thing we control with)
• The plant’s input and outputs $u(t)$ and $y(t)$ respectively
• The reference signal $r(t)$ and a disturbance (noise in the system) $d(t)$

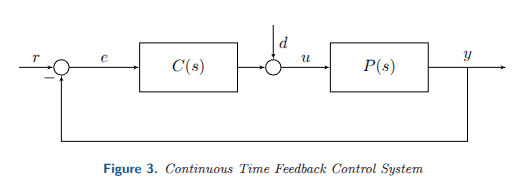
General speaking, we would

• Derive the relationships between all of the factors inside Time Domain
• Because these equations can get pretty fucked (lots of differential equations), we do a Laplace Transform to work inside the Frequency Domain
  • This lets us build state space models and theoretically derive proper control parameters that will make the system stable
    • Based on some characterization of the plant

There are many ways to make controllers, the way I was specifically taught was PID

$$u(t)=K_{p}e(t)+K_i\int e(t)dt+K_p\frac{de}{dt}$$

Which in the Laplace Domain would look something like

$$K_p+\frac{K_i}{s}+K_{d}s=\frac{K_d{s}^2+K_{p}s+K_i}{s}$$

Example

Say we want to control a mass-spring-damper system.

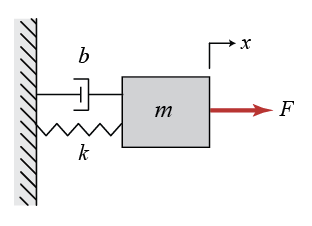
The governing equation of the system is:

$$m\dot{x}\dot{}+b\dot{x}+kx=F$$

Note: x and F are functions of time. As you can see, messy differential, so we should go into the frequency domain.

$${\to }^{\mathcal{L}}m{s}^{2}X(s)+bsX(s)+kX(s)=F(s)$$ $$\frac{X(s)}{F(s)}=\frac{1}{m{s}^2+bs+k}$$

This is a Transfer Function showing how the position of the mass varies with the force applied.

For the sake of argument, lets add some values to characterize the system easier.

$$\frac{X(s)}{F(s)}=\frac{1}{s^2+10s+20}$$

Open-loop control

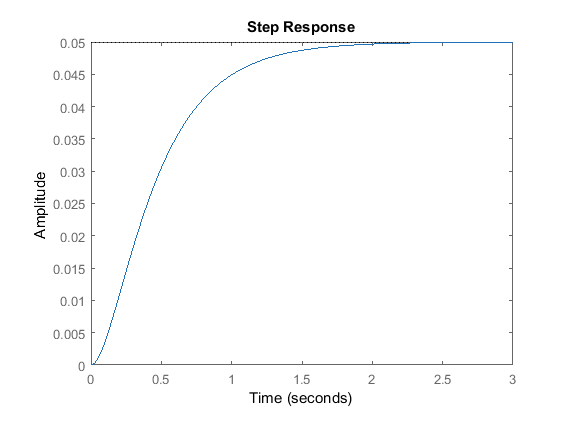Ew, too slow, let me speed it up.

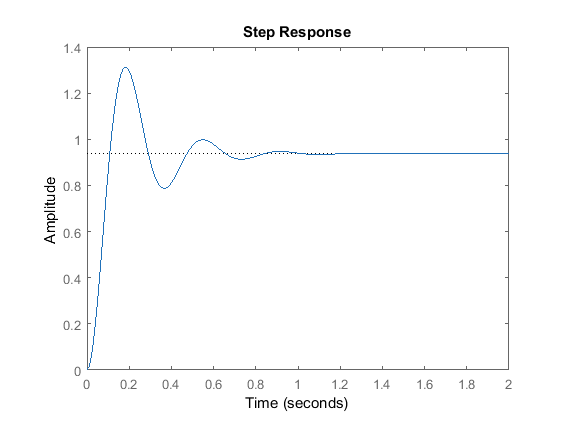
Proportional Control

We are slowly adding in aspects of out controller into the system, causing the transfer function the system the change. With proportional control, the transfer function turns into (and can be derived quite easily)

$$T(s)=\frac{X(s)}{R(s)}=\frac{K_p}{s^2+10s+(20+K_p)}$$

Proportional - Derivative Control (PD)

Lots of oscillations occurring, so lets try to limit that from happening by limiting the change in the amplitude. Adding in $K_d$ which again is easy to add into the transfer function.

$$T(s)=\frac{X(s)}{R(s)}=\frac{K_{d}s+K_p}{s^2+(10+K_d)s+(20+K_p)}$$

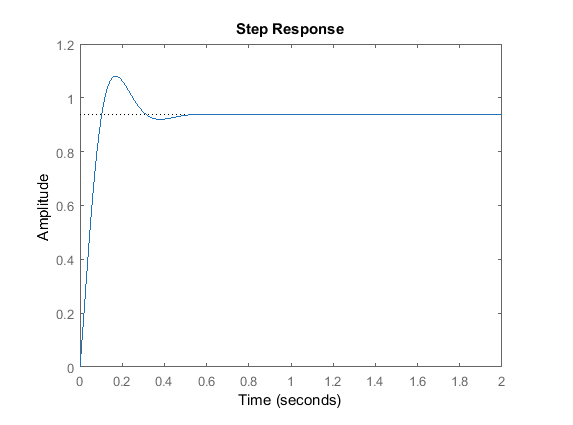
Proportional-Integral Control (PI)

This is often used where theres alot of steady state error (from disturbances usually). Use this if you dont really care about the response time.

$$T(s)=\frac{X(s)}{R(s)}=\frac{K_{p}s+K_i}{s^3+10s^2+(20+K_p)s+K_i}$$

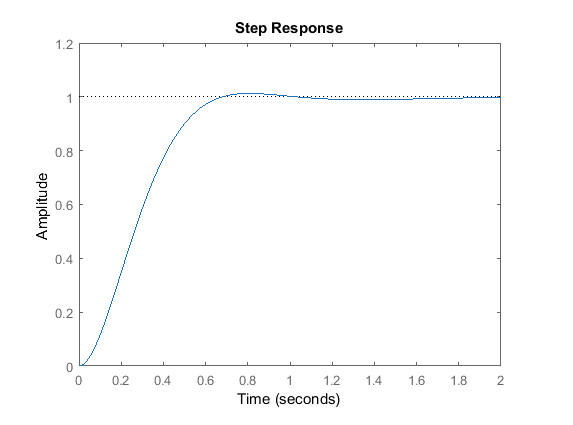
Proportional-Integral-Derivative Controller (PID)

The full package. P for quick response, D for reduce oscillations, I for reduced steady state error (generally).

$$T(s)=\frac{X(s)}{R(s)}=\frac{K_d{s}^2+K_{p}s+K_i}{s^3+(10+K_d)s^2+(20+K_p)s+K_i}$$

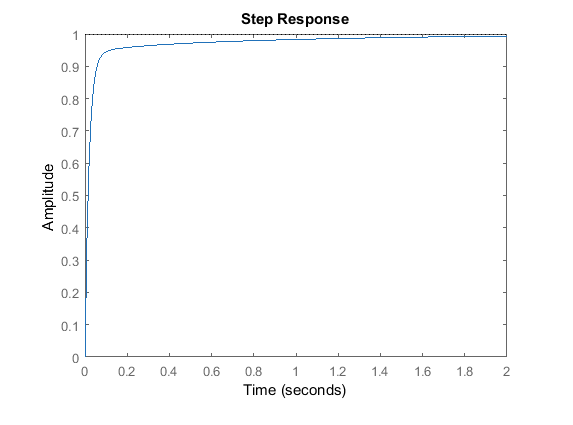
Not the only controllers

There are like a bunch of other types of controllers, all of them having their own set of equations and stuff. ie. Pure Pursuit Controller, MPPI, MPC, etc.