Stability

Continuous Time Stability

Say we have a dynamical system defined as.

$$\dot{x}=\lambda x+u,\lambda \in \mathbb{C}$$

if we take the Laplace transform, we get.

$$X(s)=\frac{1}{s-\lambda }U(s)$$

So we have setup a case where we have a transfer function with a single pole. We can use this to analyze how different values of $\lambda$ affect the signal. If we give a constant signal to the system…

Case 1: $\mathrm{Re}(\lambda )<0$

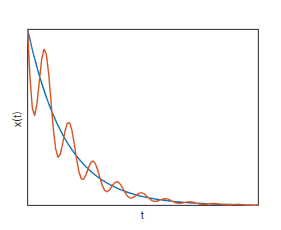
Case 2: $\mathrm{Re}(\lambda )>0$

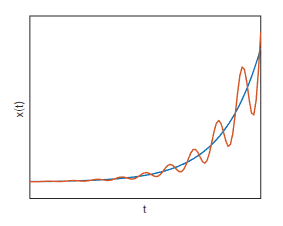Unstable!!! The pole makes the system explodes!

Case 3: $\mathrm{Re}(\lambda )=0$

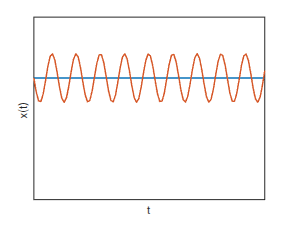
Conclusion

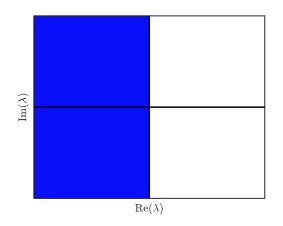
In continuous time, a real, rational, transfer function $P(s)$ is stable if all the poles $\mathrm{Re}(\lambda )<0$ so they lie in the Open Left Hand Plane (OLHP) of the Imaginary Plane

Discrete Time Stability

Now what about discrete time…

We can setup a similar experiment in discrete time with

$$x^{+}=\lambda x$$ $$|x[k]|=|\lambda {|}^k|x[0]|$$

Taking the Z-transform

$$X[z]=\frac{1}{z-\lambda }U[z]$$

We can witness the effects of $\lambda$ in discrete time.

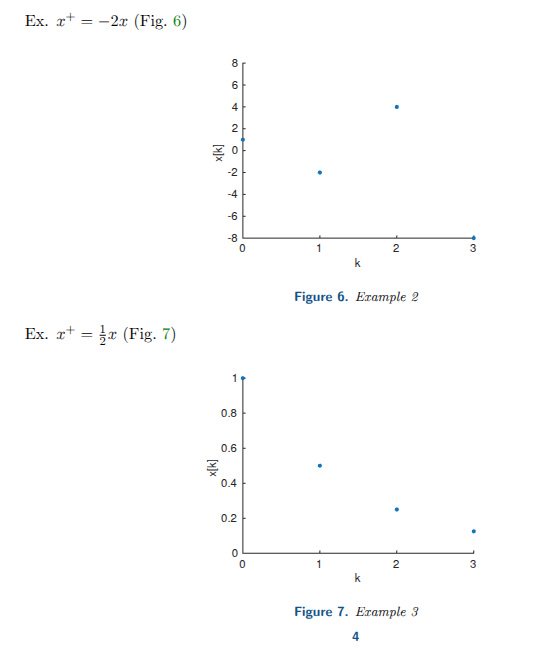This is telling us that the moment $|\lambda |\ge 1$ we reach instability.

We say that at $|\lambda |=1$ is unstable because in practice its really hard to stay at 1. Its more of a convention thing.

Conclusion

In discrete time, **a real, rational, transfer function $G[z]$ is stable if all the poles $|\lambda |<1$ so they lie in the Open Unit Disk

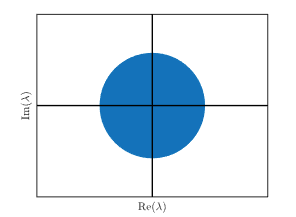
Conclusion

Mixing the two together…

A real, rational transfer function $P(s)/G[z]$ is stable if all poles of $P(s)/G[z]$ lie in ${\mathbb{C}}^{-}$ (The OLHP) / $\mathbb{D}$ (The Open Unit Disk).

^^ This is two statements combined into one, OHLP is for continuous, OUD is for discrete.