Multivariate Gaussian

probability

For review of multivariate calculus, see 00 - Multivariate Calculus Table of Contents.

Normal Distribution (Gaussian) in 1D

Given by

$$p(x)\sim \mathcal{N}(\mu ,{\sigma }^2)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left(-\frac{1}{2}{\left(\frac{x-\mu }{\sigma }\right)}^2\right)$$

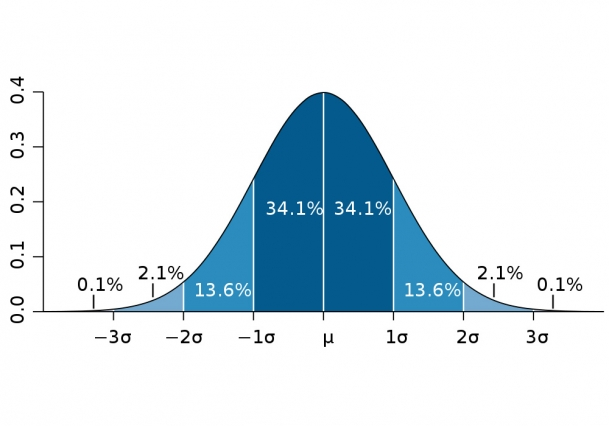
• The higher the $\sigma$ the “wider the distribution”
• $\sigma$ is the standard deviation, ${\sigma }^2$ is the variance

Multivariate Gaussian

Given by

$$p(\mathbf{x})\sim \mathcal{N}(\mathbf{\mu },\Sigma )=\frac{1}{(2\pi {)}^{d/2}{\Sigma }^{1/2}}\exp \left(-\frac{1}{2}(\mathbf{x}-\mathbf{\mu }{)}^T{\Sigma }^{-1}(\mathbf{x}-\mathbf{\mu })\right)$$

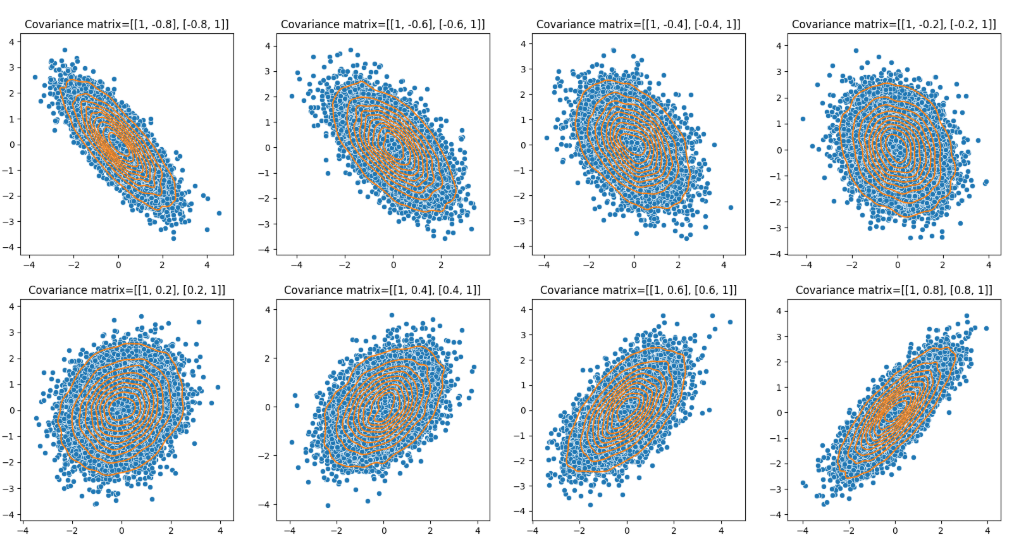Where $\Sigma$ is called the covariance matrix, it consists of the following:

• Diagonal $\Sigma$ variance in each dimension
• Off Diagonal $\Sigma$ covariance between two dimensions

$$\Sigma =\left(\begin{array}{cc}Var(X)& Cov(X,Y)\\ Cov(Y,X)& Var(Y)\end{array}\right)$$

A covariance matrix is, by definition, symmetric.

$$Cov(Y,X)=E[(Y-{\mu }_Y)(X-{\mu }_X)]=E[(X-{\mu }_X)(Y-{\mu }_Y)]=Cov(X,Y)$$

Linear Change in a Gaussian

We have

$$\mathbf{x}\sim \mathcal{N}({\mathbf{\mu }}_{\mathbf{x}},{\Sigma }_{xx})=\frac{1}{(2\pi {)}^{d/2}{\Sigma }^{1/2}}\exp \left(-\frac{1}{2}(\mathbf{x}-\mathbf{\mu }{)}^T{\Sigma }^{-1}(\mathbf{x}-\mathbf{\mu })\right)$$

It can be shown that if we have a linear transformation

$$\mathbf{y}=\mathbf{Gx}$$

The resultant Gaussian is

$$y\sim \mathcal{N}({\mu }_y,{\Sigma }_{yy})=\mathcal{N}(\mathbf{G}{\mu }_x,\mathbf{G}{\Sigma }_{xx}{\mathbf{G}}^T)$$

Non-Linear Operations on Gaussians

There isn't a nice way of doing something like with with non-linear functions, so we Linearize by approximating a Jacobian near the point of operation

given a non-linear function

$$\mathbf{y}=g(\mathbf{x})+vv\sim \mathcal{N}(0,\mathbf{R})$$

where $\mathbf{R}$ is the measurement noise covariance we linearize like

$$g(\mathbf{x})\simeq {\mu }_y+\mathbf{G}(\mathbf{x}-{\mathbf{\mu }}_x)$$ $$\mathbf{G}=\frac{\partial g(\mathbf{x})}{\partial \mathbf{x}}{|}_{\mathbf{x}={\mu }_x}$$ $${\mu }_y=g({\mu }_x)$$

It can be shown with some work that the resultant

$$\mathbf{y}\sim \mathcal{N}({\mathbf{\mu }}_y,{\mathbf{\Sigma }}_{yy})=\mathcal{N}(g({\mathbf{\mu }}_x),\mathbf{R}+\mathbf{G}{\Sigma }_{xx}{\mathbf{G}}^T)$$

Normalized Product of Gaussians

The normalized product of N gaussians is also a gaussian. Without normalization, we still end up with gaussian shape, just scaled by a constant.

$$\exp \left(-\frac{1}{2}(\mathbf{x}-\mathbf{\mu }{)}^T{\Sigma }^{-1}(\mathbf{x}-\mathbf{\mu })\right)=\eta \prod _{k=1}^K\exp \left(-\frac{1}{2}(\mathbf{x}-{\mathbf{\mu }}_{\mathbf{k}}{)}^T{\Sigma }_k^{-1}(\mathbf{x}-{\mathbf{\mu }}_{\mathbf{k}})\right)$$ $${\Sigma }^{-1}=\sum _{k=1}^K{\Sigma }_k^{-1}$$ $${\Sigma }^{-1}\mu =\sum _{k=1}^K{\Sigma }_k^{-1}{\mu }_k$$