Poses and Transformations

The translation and rotation of a body 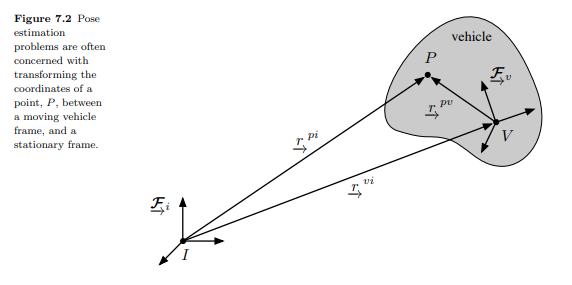Following from Rotation Representations and 3D Numanclature

$${\mathbf{r}}_i^{pi}={\mathbf{C}}_{iv}{\mathbf{r}}_v^{pv}+{\mathbf{r}}_i^{vi}$$

We refer to the pose as

$$\{{\mathbf{r}}_i^{vi},{\mathbf{C}}_{iv}\}$$

Transformation Matrices

Following ${\mathbf{r}}_i^{pi}={\mathbf{C}}_{iv}{\mathbf{r}}_v^{pv}+{\mathbf{r}}_i^{vi}$ , we can express this is a convenient form:

\begin{bmatrix} \mathbf{r}_{i}^{pi} \\ 1 \end{bmatrix} =\underbrace{ \begin{bmatrix} \mathbf{C}_{iv} & \mathbf{r}_{i}^{vi} \\ \mathbf{0}^{T} & 1 \end{bmatrix} }_{ \mathbf{T}_{iv} }\begin{bmatrix} \mathbf{r}_{v}^{pv} \\ 1 \end{bmatrix}$$ Where $\mathbf{T}_{iv} \in \mathbb{R}^{4\times4}$ is known as the **Transformation Matrix**. >[!info] To make this transformation possible, we have to turn points to their **homogeneous representation** > **To go the other way, we require an inverse transformation matrix**

\begin{bmatrix} \mathbf{r}{v}^{pv} \ 1 \end{bmatrix}=\mathbf{T}{iv}^{-1}\begin{bmatrix} \mathbf{r}_{i}^{pi} \ 1 \end{bmatrix}

\mathbf{T}_{vi}^{-1} = \begin{bmatrix} \mathbf{C}_{vi} & \mathbf{r}_i^{vi} \\ \mathbf{0}^T & 1 \end{bmatrix}^{-1} = \begin{bmatrix} \mathbf{C}_{vi}^T & -\mathbf{C}_{iv}^T \mathbf{r}_i^{vi} \\ \mathbf{0}^T & 1 \end{bmatrix} = \begin{bmatrix} \mathbf{C}_{iv} & -\mathbf{r}_v^{iv} \\ \mathbf{0}^T & 1 \end{bmatrix} = \mathbf{T}_{iv} $$ We can also chain transformation matricies together $$ \mathbf{T}_{iv}=\mathbf{T}_{ia}\mathbf{T}_{ab}\mathbf{T}_{bv} $$ With all the subscripts removed, by convention we define a transformation matrix as. $$ \mathbf{T}=\begin{bmatrix} \mathbf{C} & \mathbf{r} \\ \mathbf{0}^{T} & 1 \end{bmatrix} $$ Which is the basis of [[SE(3)]]