Rotation Representations

Given a reference frame or vector defined as from 3D Numanclature

$$\overrightarrow{{\mathcal{F}}_i}=\left[\begin{array}{c}{\vec{1}}_{1,i}\\ {\vec{1}}_{2,i}\\ {\vec{1}}_{3,i}\end{array}\right]\overrightarrow{r_i}=\left[\begin{array}{c}{\vec{1}}_{1,i}{r}_1\\ {\vec{1}}_{2,i}{r}_2\\ {\vec{1}}_{3,i}{r}_3\end{array}\right]$$

Rotation Matrix

$$\mathbf{C}\in {\mathbb{R}}^{3\times 3}$$

Able to perform a rotation on a vector $\mathbf{r}$ such that

$${\mathbf{r}}_1={\mathbf{C}}_{21}^{-1}{\mathbf{r}}_2={\mathbf{C}}_{12}{\mathbf{r}}_2{\mathbf{r}}_2={\mathbf{C}}_{21}{\mathbf{r}}_1$$ $${\mathbf{r}}_3={\mathbf{C}}_{32}{\mathbf{r}}_2={\mathbf{C}}_{32}{\mathbf{C}}_{21}{\mathbf{r}}_1\text{therefore}{\mathbf{C}}_{31}={\mathbf{C}}_{32}{\mathbf{C}}_{21}$$

So you can chain them!

Euler Angles

Two types of euler representations.

3($\phi$)-1($\gamma$)-3($\theta$)

Consists of a rotation about the 3-axis, and then the 1-axis, and then the transformed 3 axis.

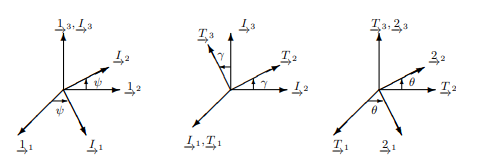
$\theta$ is spin angle $\gamma$ is nutation angle $\phi$ is precession angle

To convert it to a rotation matrix:

$${\mathbf{C}}_{21}(\theta ,\gamma ,\psi )={\mathbf{C}}_{2J}{\mathbf{C}}_{J1}{\mathbf{C}}_{11}$$ $$={\mathbf{C}}_3(\theta ){\mathbf{C}}_1(\gamma ){\mathbf{C}}_3(\psi )$$ $$=\left[\begin{array}{ccc}{c}_{\theta }{c}_{\psi }-s_{\theta }{c}_{\gamma }{s}_{\psi }& s_{\theta }{c}_{\theta }+c_{\gamma }{s}_{\theta }{c}_{\psi }& s_{\gamma }{s}_{\psi }\\ -c_{\psi }{s}_{\theta }-c_{\theta }{c}_{\gamma }{s}_{\psi }& -s_{\theta }{s}_{\psi }+c_{\theta }{c}_{\gamma }{c}_{\psi }& s_{\gamma }{c}_{\psi }\\ s_{\psi }{s}_{\gamma }& -s_{\gamma }{c}_{\psi }& c_{\gamma }\end{array}\right]$$

have made the abbreviations $s=\sin$, $c=\cos$

1(${\theta }_1$)-2(${\theta }_2$)-3(${\theta }_3$)

Consists of a rotation in the 1-axis, then the 2-axis, and finally the 3-axis

To convert to rotation matrix

$${\mathbf{C}}_{21}({\theta }_3,{\theta }_2,{\theta }_1)={\mathbf{C}}_3({\theta }_3){\mathbf{C}}_2({\theta }_2){\mathbf{C}}_1({\theta }_1)$$ $$=\left[\begin{array}{ccc}{c}_2{c}_3& c_1{s}_3+s_1{s}_2{c}_3& s_1{s}_3-c_1{s}_2{c}_3\\ -c_2{s}_3& c_1{c}_3-s_1{s}_2{s}_3& s_1{c}_3+c_1{s}_2{s}_3\\ s_2& -s_1{c}_2& c_1{c}_2\end{array}\right]$$

All Euler sequences have singularities. That is, a point in which you lose one degree of freedom because two of the axes of rotation are the same. This is known a gimbal lock (or in more math terms you've reached a singularity)

The term gimbal lock comes from the fact that a gimbal measurement device (like an IMU) is rotated in space such that two of the gimbal rings line up. They seemingly get stuck together because of physics and all of the sudden our IMU loses a degree of freedom to measure with.

https://www.youtube.com/watch?v=oj7v3MXJL3M At this point in time of the gimbal, two axes line up and you end up with infinite gimbal states that could give you the rotation of the spinning core. This is bad because our gimbal IMU reading starts to go crazy.

In rotational geometry, this is referred to as reaching a singularity. For 1-2-3, this happens when ${\theta }_2=\frac{\pi }{2}$

When trying to convert into a rotation matrix, we get:

$${\mathbf{C}}_{21}({\theta }_3,\frac{\pi }{2},{\theta }_1)=\left[\begin{array}{ccc}0& \sin ({\theta }_1+{\theta }_3)& -\cos ({\theta }_1+{\theta }_3)\\ 0& \cos ({\theta }_1+{\theta }_3)& \sin ({\theta }_1+{\theta }_3)\\ 1& 0& 0\end{array}\right]$$

As a result, when we want to recover euler angles from a rotation matrix, we no longer have a unique solution for ${\theta }_1,{\theta }_3$

All Euler Angles have a singularity.

Infinitesimal Rotations

For small 1-2-3 transformations, we can approximate the rotation matrix as

$${\mathbf{C}}_{21}=\left[\begin{array}{ccc}1& {\theta }_3& -{\theta }_2\\ -{\theta }_3& 1& {\theta }_1\\ {\theta }_2& -{\theta }_1& 1\end{array}\right]=1-{\theta }^{\times }$$

Euler Parameters

From Euler’s Rotation Theorem , the most general motion of a rigid body with one point fixed is a rotation about an axis through that point.

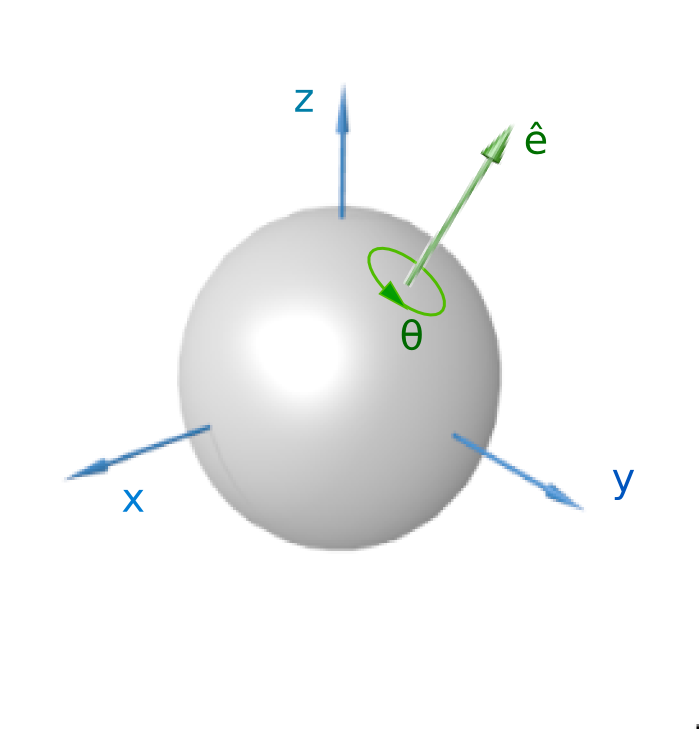
For our case, we define that axis as a unit vector

$$\mathbf{a}={\left[\begin{array}{ccc}{a}_1& a_2& a_3\end{array}\right]}^T{\mathbf{a}}^T\mathbf{a}=1$$

The angle of rotation is defined as $\varphi$

A rotation matrix is given by

$${\mathbf{C}}_{21}=\cos \varphi 1+(1-\cos \varphi )\mathbf{a}{\mathbf{a}}^T-\sin \varphi {\mathbf{a}}^{\times }$$

Euler parameters are defined from this:

$$\eta =\cos \frac{\varphi }{2}ϵ=\mathbf{a}\sin \frac{\varphi }{2}=\left[\begin{array}{c}{a}_1\sin \left(\frac{\varphi }{2}\right)\\ a_2\sin \left(\frac{\varphi }{2}\right)\\ a_3\sin \left(\frac{\varphi }{2}\right)\end{array}\right]=\left[\begin{array}{c}{ϵ}_1\\ {ϵ}_2\\ {ϵ}_3\end{array}\right]$$

These parameters are not independant because

$${\eta }^2+{ϵ}_1^2+{ϵ}_2^2+{ϵ}_3^2=1$$

Stacked as $\mathbf{q}=\left[\begin{array}{c}ϵ\\ \eta \end{array}\right]$ gives us quarternions

Quarternions

Follows from [Euler Parameters](#Euler Parameters)

$$\mathbf{q}=\left[\begin{array}{c}ϵ\\ \eta \end{array}\right]$$

There are special kinds of operators on quarternions called the left-hand and right hand compound operators.

$${\mathbf{q}}^{+}=\left[\begin{array}{cc}\eta 1-{ϵ}^{\times }& ϵ\\ -{ϵ}^T& \eta \end{array}\right]{\mathbf{q}}^{\oplus }=\left[\begin{array}{cc}\eta 1+{ϵ}^{\times }& ϵ\\ -{ϵ}^T& \eta \end{array}\right]$$

And the inverse operator is defined explicitly for quarternions to be

$${\mathbf{q}}^{-1}=\left[\begin{array}{c}-ϵ\\ \eta \end{array}\right]$$

Some useful identities with these operators…

Quarternions form a non-commutative group under both the $\oplus +$ operators. With the identity element of the group being

$$\iota =\left[\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right]{\iota }^{+}={\iota }^{\oplus }=1$$

Rotating with a Quarternion

given a point (in homogeneous form)

$$\mathbf{v}=\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$$

We can rotate it using the quarterion, $\mathbf{q}$, by

$$\mathbf{u}={\mathbf{q}}^{+}{\mathbf{v}}^{+}{\mathbf{q}}^{-1}={\mathbf{q}}^{+}{\mathbf{q}}^{-1\oplus }\mathbf{v}=\mathbf{Rv}$$

If just so follows that we end up with SO(3) by getting $\mathbf{R}$

$$\mathbf{R}={\mathbf{q}}^{+}{\mathbf{q}}^{-1\oplus }={\mathbf{q}}^{-1\oplus }{\mathbf{q}}^{+}={\mathbf{q}}^{{\oplus }^T}{\mathbf{q}}^{+}=\left[\begin{array}{cc}\mathbf{C}& 0\\ 0^{\mathbf{T}}& 1\end{array}\right]$$

Gibbs Vector

$$\mathbf{g}=\mathbf{a}\tan \frac{\varphi }{2}$$

Has a singularity at $\frac{\pi }{2}$.

Less common, but worth noting.