Rotational Kinematics

Using what we discussed in Rotation Representations

Angular Velocity

The angular velocity of frame 2 with respect to frame 1 is denoted as $\overrightarrow{{\omega }_{21}}$ The angular velocity of frame 1 with respect to frame 2 is denoted as $\overrightarrow{{\omega }_{12}}=-\overrightarrow{{\omega }_{21}}$

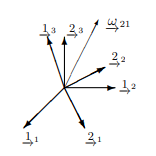
Important Applications

A vector time derivative is the instantaneous rate of change of a vector. Different frames of reference see different motion so we need to analyze the motion of two different frames separately.

In Frame 1

We can define the vector time derivative in frame 1 as $\dot{(\cdot )}$. Hence the vector time derivative in frame 1 of frame 1 itself is nothing

$${\dot{\vec{\mathcal{F}}}}_1=\vec{0}$$

Given a angular velocity, $\overrightarrow{{\omega }_{21}}$, the vector time derivative of frame 2 is given by

$${\dot{\vec{\mathcal{F}}}}_2=\overrightarrow{{\omega }_{21}}\times {\vec{\mathcal{F}}}_2$$

Say we have a vector expressed in both frames

$$\vec{r}={\vec{\mathcal{F}}}_1^T{\mathbf{r}}_1={\vec{\mathcal{F}}}_2^T{\mathbf{r}}_2$$

The time derivative of such vector from the perspective of Frame 1 is

$$\dot{\vec{r}}=\text{cancelto}0{\dot{\vec{\mathcal{F}}}}_1^T{\mathbf{r}}_1+{\vec{\mathcal{F}}}_1^T\dot{{\mathbf{r}}_1}={\vec{\mathcal{F}}}_1^T\dot{{\mathbf{r}}_1}$$

In Frame 2

We will define the vector time derivative in frame 2 as $\mathring{(\cdot )}$.

$$\mathring{\stackrel{⃗}{r}}=\text{cancelto}0{\mathring{\stackrel{⃗}{\mathcal{F}}}}_2^T{\mathbf{r}}_2+{\vec{\mathcal{F}}}_2^T\mathring{{\mathbf{r}}_2}={\vec{\mathcal{F}}}_2^T\mathring{{\mathbf{r}}_2}$$

Combining Perspectives (Relationship of Vector Time Derivative)

$${\vec{\mathcal{F}}}_2^T{\dot{\mathbf{r}}}_2={\vec{\mathcal{F}}}_2^T{\mathring{\mathbf{r}}}_2{\dot{\mathbf{r}}}_2={\mathring{\mathbf{r}}}_2$$

The vector time derivative of $\vec{r}$ in expressed in terms of frame 2 but as seen in frame 1 is given by

$$\dot{\vec{r}}=\mathring{\stackrel{⃗}{r}}+{\vec{\omega }}_{21}\times \vec{r}$$

This is telling us how the time derivative of a vector witnessed between two different frames changes based on the angular velocity between two different frames

Inertial Time Derivative

A useful application is when we detect something in a moving frame, and we want to transform it to a non-rotating inertial reference frame (a frame that does not rotate or accelerate, it is often something like the map origin or map reference frame).

Say our rotating frame ${\vec{\mathcal{F}}}_2$ is undergoing a angular velocity ${\vec{\omega }}_{21}$.

First we express the angular velocity

$${\vec{\omega }}_{21}={\vec{\mathcal{F}}}_2^T{\omega }_2^{21}$$

We detected an object in Frame 2 with position ${\vec{\mathcal{F}}}_2^T{\mathbf{r}}_2$ . Because Frame 2 is undergoing an angular velocity, the change in the position of the object in the non-rotation inertial frame is given by

Acceleration

A similar formula can be derived for acceleration

$$\ddot{\vec{r}}=\mathring{\stackrel{˚}{\stackrel{⃗}{r}}}+2{\vec{\omega }}_{21}\times \mathring{\stackrel{⃗}{r}}+{\mathring{\stackrel{⃗}{\omega }}}_{21}\times \vec{r}+{\vec{\omega }}_{21}\times ({\vec{\omega }}_{21}\times \vec{r})$$ $$\ddot{{\mathbf{r}}_1}={\mathbf{C}}_{12}[\ddot{{\mathbf{r}}_2}+2{\mathbf{\omega }}_2^{21\times }\dot{\mathbf{r}}+{\dot{\mathbf{\omega }}}_2^{21\times }{\mathbf{r}}_2+{\mathbf{\omega }}_2^{21\times }{\mathbf{\omega }}_2^{21\times }{\mathbf{r}}_2]$$

note that we are only looking at the instantaneous velocities and accelerations of $\vec{r}$ when the two reference frames are on top of each other and frame 2 in induced with a angular velocity

Angular Velocity Given Rotation Matrix

When our rotation matrix is given as a function of time, our angular velocity is given by:

$${\mathbf{\omega }}_2^{21\times }=-{\dot{\mathbf{C}}}_{21}{\mathbf{C}}_{21}^{-1}=-{\dot{\mathbf{C}}}_{21}{\mathbf{C}}_{21}^T$$