Bayes Filter

see NLNG Problem Statement

The Bayes filter seeks to come up with an entire PDF to represent the likelihood of state ${\mathbf{x}}_k$, using only the measurements up to and including the current time. This is shown as the notation

$$p({\mathbf{x}}_k|{\check{\mathbf{x}}}_0,{\mathbf{v}}_{1:k},{\mathbf{y}}_{0:k})$$

Because NLNG Problem Statement is Markovian, we have independence between measurements, so we can factor out the current measurement.

$$p({\mathbf{x}}_k|{\check{\mathbf{x}}}_0,{\mathbf{v}}_{1:k},{\mathbf{y}}_{0:k})=\eta p({\mathbf{y}}_k|{\mathbf{x}}_k)p({\mathbf{x}}_k|{\check{\mathbf{x}}}_0,{\mathbf{v}}_{1:k},{\mathbf{y}}_{0:k-1})$$

If we integrate over all possible values of ${\mathbf{x}}_{k-1}$ we get

$$p({\mathbf{x}}_k|{\check{\mathbf{x}}}_0,{\mathbf{v}}_{1:k},{\mathbf{y}}_{0:k-1})=\int p({\mathbf{x}}_k,{\mathbf{x}}_{k-1}|{\check{\mathbf{x}}}_0,{\mathbf{v}}_{1:k},y_{0:k-1})d{\mathbf{x}}_{k-1}$$ $$=\int p({\mathbf{x}}_k|{\mathbf{x}}_{k-1},{\check{\mathbf{x}}}_0,{\mathbf{v}}_{1:k},y_{0:k-1})p({\mathbf{x}}_{k-1}|{\check{\mathbf{x}}}_0,{\mathbf{v}}_{1:k},y_{0:k-1})d{\mathbf{x}}_{k-1}$$

Taking advantage of Markovian property again.

$$p({\mathbf{x}}_k|{\mathbf{x}}_{k-1},{\check{\mathbf{x}}}_0,{\mathbf{v}}_{1:k},y_{0:k-1})=p({\mathbf{x}}_k|{\mathbf{x}}_{k-1},{\mathbf{v}}_k)$$ $$p({\mathbf{x}}_{k-1}|{\check{\mathbf{x}}}_0,{\mathbf{v}}_{1:k},y_{0:k-1})=p({\mathbf{x}}_{k-1}|{\check{\mathbf{x}}}_0,{\mathbf{v}}_{1:k-1},{\mathbf{y}}_{0:k-1})$$

Which leads us to the Bayes Filter

$$\underset{\text{posterior belief}}{\underbrace{p({\mathbf{x}}_k|{\check{\mathbf{x}}}_0,{\mathbf{v}}_{1:k},{\mathbf{y}}_{0:k})}}=\eta \underset{\begin{array}{c}\text{observation}\\ \text{correction}\\ \text{using}\mathbf{g}(\cdot )\end{array}}{\underbrace{p({\mathbf{y}}_k|{\mathbf{x}}_k)}}\int \underset{\begin{array}{c}\text{motion prediction}\\ \text{using }\mathbf{f}(\cdot )\end{array}}{\underbrace{p({\mathbf{x}}_k|{\mathbf{x}}_{k-1},{\mathbf{v}}_k)}}\underset{\text{prior belief}}{\underbrace{p({\mathbf{x}}_{k-1}|{\check{\mathbf{x}}}_0,{\mathbf{v}}_{1:k-1},{\mathbf{y}}_{0:k-1})}}d{\mathbf{x}}_{k-1}$$

This is nothing more than a mathematical artifact that provides a fundamental high-level reasoning for why these recursive state estimation filters work.

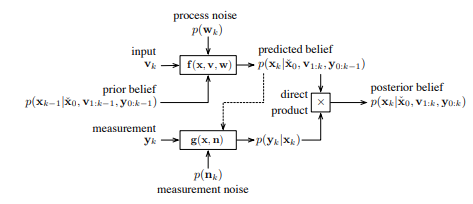
The Bayes filter tells us that optimal state estimation is a two-step recursive process:

1. Prediction Step uses the motion model to propagate the prior belief forward
2. Correction Step uses observations to refine our belief. The resultant final belief is a product of the two.

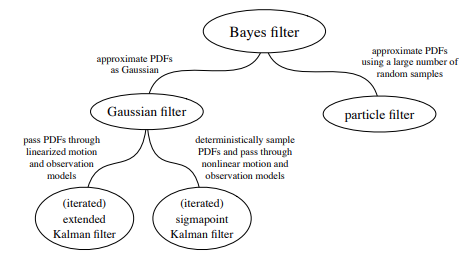
Key things to note

1. PDFs live in infinite-dimensional space, and as such an infinite amount of memory is needed to represent our belief. To deal with this issue, we can
   1. approximate these PDFs as Gaussians, or
   2. using a finite number of random samples.
2. The integral of the Bayes Filter is extremely computational expensive. To make this evaluation easier, we often
   1. linearize the motion and observation models
   2. employ monte-carlo integration

Its important to keep in mind that fundamentally these recursive algorithms, and what they strive for which is to better approximate the Bayes Filter, fall under one major assumption and that's that the state estimation problem is fundamentally a Markovian

One such method of trying handle these problems is the Extended Kalman Filter

This provides us a basis for deriving recursive filters that stem from the Generalized Gaussian Filter as well as Particle Filter