This is one of the only practical techniques to handing non-Gaussian noise and non-linear observation and motion models. We don't need to to have any analytical expressions for and !
This is an approximation of Bayes Filter. Reminder
The method shown here is sometimes called the bootstrap algorithm, condensation algorithm, or survival-of-the-fittest algorithm
How it Works
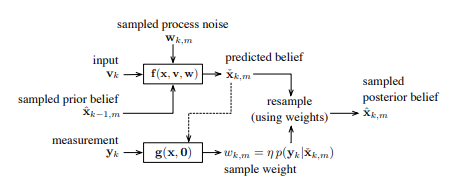
- Draw M samples from the joint density comprising the prior and motion noise
where $m$ is the unique *particle index*. In practice we just draw samples from the two factors separately
2. Generate a prediction of the posterior by sending the samples through the motion model
these new *predicted particles* together approximate the posterior density, $p(\mathbf{x}_{k}|\check{\mathbf{x}}_{0},\mathbf{v}_{1:k},\mathbf{y}_{1:k-1})$
3. Correct the posterior PDF by incorporating (our measurements). This is done in two steps: 1. Assign a scalar weight to each predicted particle based on the divergence between the desired posterior and the predicted posterior for each particle.
This is done in practice normally by simulating a **expected sensor reading** using the non-linear observation model.
and then set $p(\mathbf{y}_{k}|\check{\mathbf{x}}_{k,m})=p(\mathbf{y}_{k}|\check{\mathbf{y}}_{k,m})$
2. Resample the posterior based on the weight assigned to each predicted posterior particle:
**There are a number of ways to do this resampling**
here can be fed back into step 2!!! ⇐ bad representation, but I'm trying to say that the samples you redrew here are fed inot the motion model again. (the noise is also resampled)
- Repeat steps 1-3 until we want to stop. ie. maybe when
Methods of Resampling
Resampling the posterior density according to the weights we get is pretty important, and there are a number of ways to do it.
Madow Resampling
Assuming we have samples, each assigned an unnormalized weight . From the weights, we create bins with boundary according to
This defines boundaries of M bins between 0 and 1.
def madow_systematic_resampling(weights, M):
"""
Madow's systematic resampling for particle filters.
Parameters:
-----------
weights : array-like, shape (M,)
Unnormalized or normalized weights for M particles
M : int
Number of particles
Returns:
--------
indices : array, shape (M,)
Indices of resampled particles
"""
# Normalize weights
weights = np.asarray(weights)
w_normalized = weights / np.sum(weights)
# Compute cumulative sum to create bin boundaries β_m
beta = np.cumsum(w_normalized)
# Sample random starting point ρ from uniform [0, 1)
rho = np.random.uniform(0, 1)
# Initialize indices array
indices = np.zeros(M, dtype=int)
# Systematic sampling: step forward by 1/M at each iteration
for i in range(M):
# Current position (wraps around using modulo)
u = (rho + i / M) % 1.0
# Find which bin u falls into
# This is the index where β_{m-1} < u ≤ β_m
indices[i] = np.searchsorted(beta, u)
return indicesThis guarantees that any bin with width greater than will have a sample in it.
