Stability for Feedback Systems

Up to now, we have been characterizing the stability of just a plant. But what if we add feedback into the mix?

Setup

We have the following systems in continuous and discrete time.

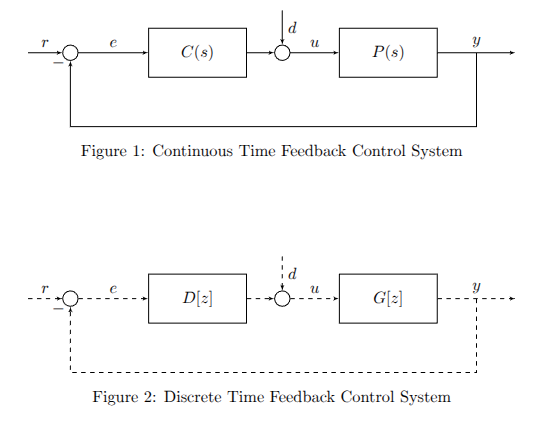
From this diagram, we have a BUNCH of Transfer functions that we are dealing with:

• $T_{ry}$ : Transfer function between the reference signal and the system output
• $T_{re}$ : Transfer function between the reference signal and the input into the controller
• $T_{ru}$ : Transfer function between the reference signal and the input to the plant
• $T_{dy}$ : Transfer function between the disturbance and the output of the system
• $T_{de}$ : Transfer function between the disturbance and the input to the controller
• $T_{du}$ : Transfer function between the disturbance and the input to the plant

THESE ARE CALLED CLOSED LOOP TRANSFER FUNCTIONS from external signals to internal ones.

Fun fact from Final Value Theorem

$$e_{ss}=\underset{k\to \infty }{\lim }e[k]=T_{re}[1]$$

You can derive all the transfer functions from first principles. They end up being the following (represented as a matrix multiplication).

Continuous Time

$$\left(\begin{array}{c}U\\ E\\ Y\end{array}\right)=\left(\begin{array}{cc}\frac{C}{1+PC}& \frac{1}{1+PC}\\ \frac{1}{1+PC}& -\frac{P}{1+PC}\\ \frac{PC}{1+PC}& \frac{P}{1+PC}\end{array}\right)\cdot \left(\begin{array}{c}R\\ D\end{array}\right)$$

Discrete Time

$$\left(\begin{array}{c}U\\ E\\ Y\end{array}\right)=\left(\begin{array}{cc}\frac{D}{1+GD}& \frac{1}{1+GD}\\ \frac{1}{1+GD}& -\frac{G}{1+GD}\\ \frac{GD}{1+GD}& \frac{G}{1+GD}\end{array}\right)\cdot \left(\begin{array}{c}R\\ D\end{array}\right)$$

A feedback system is WELL POSED if all closed-loop transfer functions from external signals to internal ones are real, rational, and proper

Definition of Closed Loop Stability

A closed-loop system is closed-loop stable if internally stable if all closed loop transfer functions from external signals to internal ones are BIBO stable.

• same as saying that for any bounded external signal ($r,d$), the corresponding internal signals ($e,u,y$) are also bounded
• $e=r-y$ (the error is given by the reference signal minus the output signal) which means that so long as $r$ and $y$ are bounded, then $e$ is bounded and thus you dont need to prove that transfer functions to e are BIBO stable because they are
• similarly $y=r-e$ so same reasoning applies
• This means that you can either prove that the transfer functions
  • (r, d) to (u, y) are all stable (and (r, d) to (e) are implied to be stable)
  • or (r, d) with (u, e) (and (r, d) to (y) are implied to be stable)